The previous blog post discussed the preprint “Ego depletion reduces attentional control: Evidence from two high-powered preregistered experiments”. Recall the preprint abstract:
“Two preregistered experiments with over 1000 participants in total found evidence of an ego depletion effect on attention control. Participants who exercised self-control on a writing task went on to make more errors on Stroop tasks (Experiment 1) and the Attention Network Test (Experiment 2) compared to participants who did not exercise self-control on the initial writing task. The depletion effect on response times was non-significant. A mini meta-analysis of the two experiments found a small (d = 0.20) but significant increase in error rates in the controlled writing condition, thereby providing clear evidence of poorer attention control under ego depletion. These results, which emerged from large preregistered experiments free from publication bias, represent the strongest evidence yet of the ego depletion effect.”
The authors mention they “found evidence”, “clear evidence”, and in fact “the strongest evidence yet”. In the previous post we focused on two pitfalls that had to do with preregistration; here we focus solely on statistical evidence, and how to quantify its strength.
Before we continue, we should acknowledge that our previous post contained at least one mistake. We mentioned that
“Concretely, when eight predictions have been preregistered (and each is tested with three dependent measures, see below), and the results yield one significant p-value at p = .028, this may not do much to convince a skeptic.”
It was pointed out to us that we overlooked the fact that one more prediction materialized: the interference is larger in the regular Stroop task than in the emotional Stroop task. We stand corrected. The source of our error is not entirely clear — perhaps we started the initial sentence as a general statement, and then adjusted it to apply more specifically to the case at hand; perhaps our interpretation of the results was colored by the outcome of Experiment 2, or by what we perceived to be most important. Regardless, this serves as a reminder that it is easy to make mistakes, particularly when one relies on a memory of what was read, even if the reading occurred relatively recently.
A Bayesian Reanalysis
Without wanting to start a lecture series on philosophy and language, it is worthwhile to consider what is meant with the word “evidence”. As Richard Morey is wont to point out during the annual JASP workshop, “evidence” is something that changes your opinion. And although a low p-value may change your opinion, the process by which this happens is informal, haphazard, and ill-defined. In contrast, the Bayesian paradigm presents a formal, precise, and coherent definition of evidence. In fact, evidence is the epistemic engine that drives the Bayesian process of knowledge updating, both for parameters and for hypotheses.
Here we will conduct Bayesian inference for the data from Experiment 1 of the ego depletion preprint, for which the authors report:
“Additionally, we found the predicted main effect of writing condition, F(1, 653) = 4.84, p = .028, ηp2 = .007, d = 0.15, such that participants made errors at a higher rate in the controlled writing condition (M = 0.064, SD = 0.046) compared to the free writing condition (M = 0.057, SD = 0.040).”
How much evidence is there? The p-value equals .028 — this is relatively close to the .05 boundary, and the paper Redefine Statistical Significance suggests that the evidence is not compelling. A JASP file that provides the Bayesian reanalysis is available on the OSF. However, the above result was not preregistered, because it did not apply the predefined exclusion criteria. For consistency, in what follows we will reanalyze the (highly similar) result that was indeed preregistered:
“After exclusions, the results reported above remained unchanged. Most importantly, the main effect of writing condition on error rates remained statistically significant, F(1, 610) = 5.17, p = .023, ηp2 = .008, d = 0.15, with participants committing errors at a higher rate in controlled writing condition (M = 0.061, SD = 0.036) compared to the free writing condition (M = 0.055, SD = 0.036).”
From the descriptive information and the fact that there were 299 participants left in the controlled writing condition and 315 in the free writing condition we can obtain the associated t-value (i.e., t = 2.064); next, we use the Summary Stats module in JASP (jasp-stats.org, see also Ly et al, 2017) to conduct three Bayesian reanalyses, presented in order of increasing informativeness. The matching JASP file is available on the OSF. We emphasize that the first two analyses are included mainly to demonstrate, perhaps ad nauseam, that p-just-below-.05 results are evidentially weak, under a wide range of default priors. The third analysis features a highly informed prior that was constructed based on existing meta-analyses of the ego depletion effect. One might therefore argue that, as far as this specific case is concerned, the third analysis is the most appropriate.
Analysis I: The Two-Sided Default
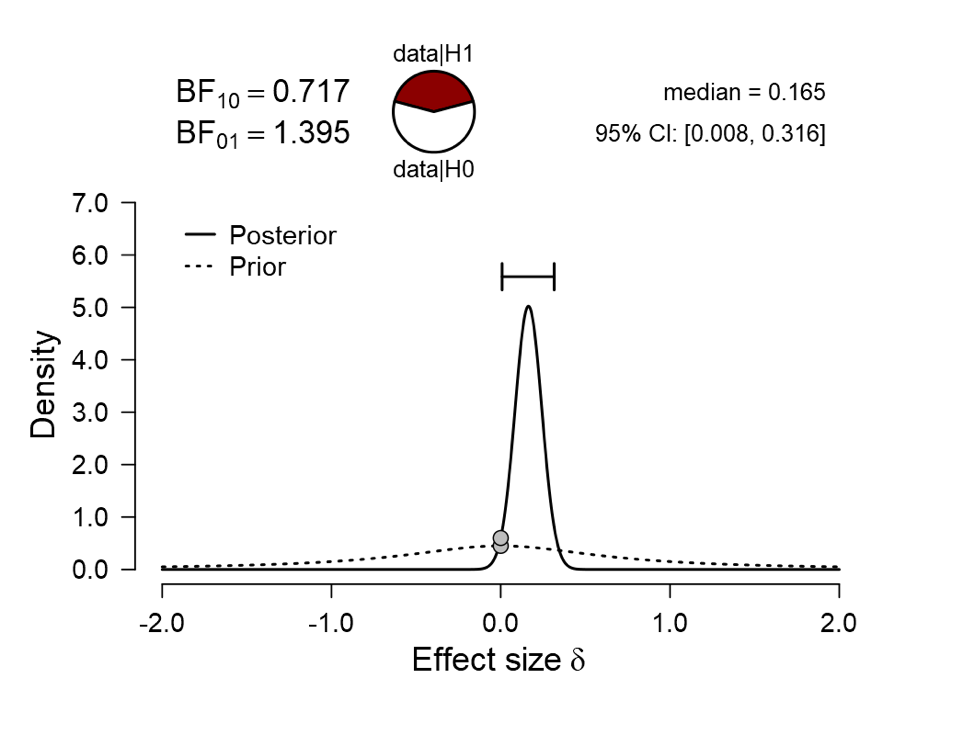
In the first analysis, we execute a t-test that contrasts the predictive performance of the null hypothesis against that of the alternative hypothesis, where effect size is assigned a default two-sided Cauchy prior distribution (for details see Ly et al., 2016; Morey & Rouder, 2015). The result:
The Bayes factor is close to 1, indicating that both models predicted the observed data about equally well, and the result is not diagnostic.
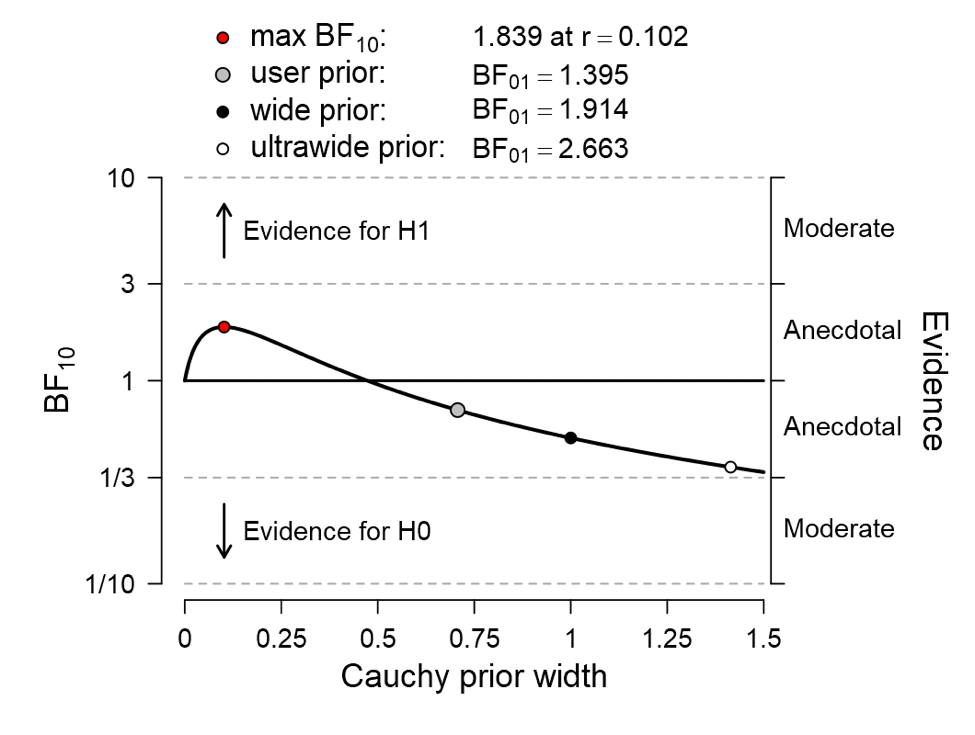
Next one may wonder how robust this result is to changes in the width of the prior distribution. One mouse click in JASP provides the answer:
The figure shows that, regardless of the width of the prior distribution, the evidence is never much in favor of the alternative hypothesis; cherry-picking the prior width yields a Bayes factor of no more than 1.84, still hardly diagnostic.
Analysis II: The One-Sided Default
One may object to the preceding analysis and argue that the alternative hypothesis ought to respect the directionality of the proposed effect. In JASP, one-sided analyses can be executed with a single mouse click. This is the result for the one-sided test with a default prior width:
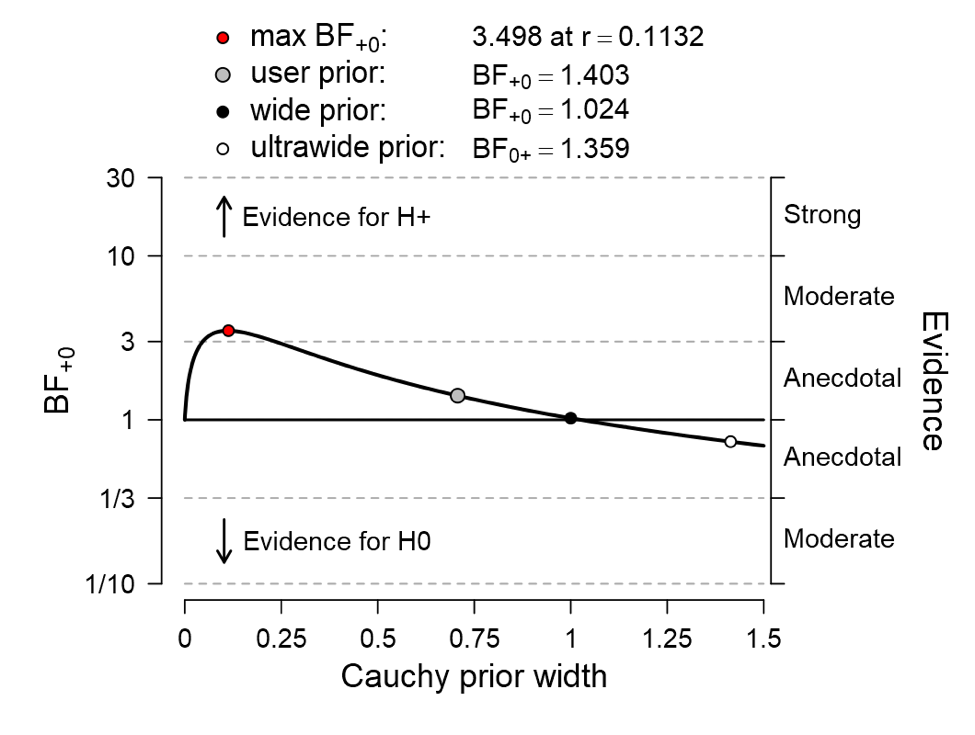
The Bayes factor remains near 1, which means that the data remain nondiagnostic. Another mouse click yields the one-sided robustness check in which the evidence is shown as a function of the prior width:
Again, the data are not compelling. When the width of the Cauchy prior distribution is cherry-picked to be about r = .11, the resulting Bayes factor is about 3.5; under equal prior probability, this leaves 1 – 3.5/4.5 = 22% for the null hypothesis.
Analysis III: The One-Sided Informed Prior
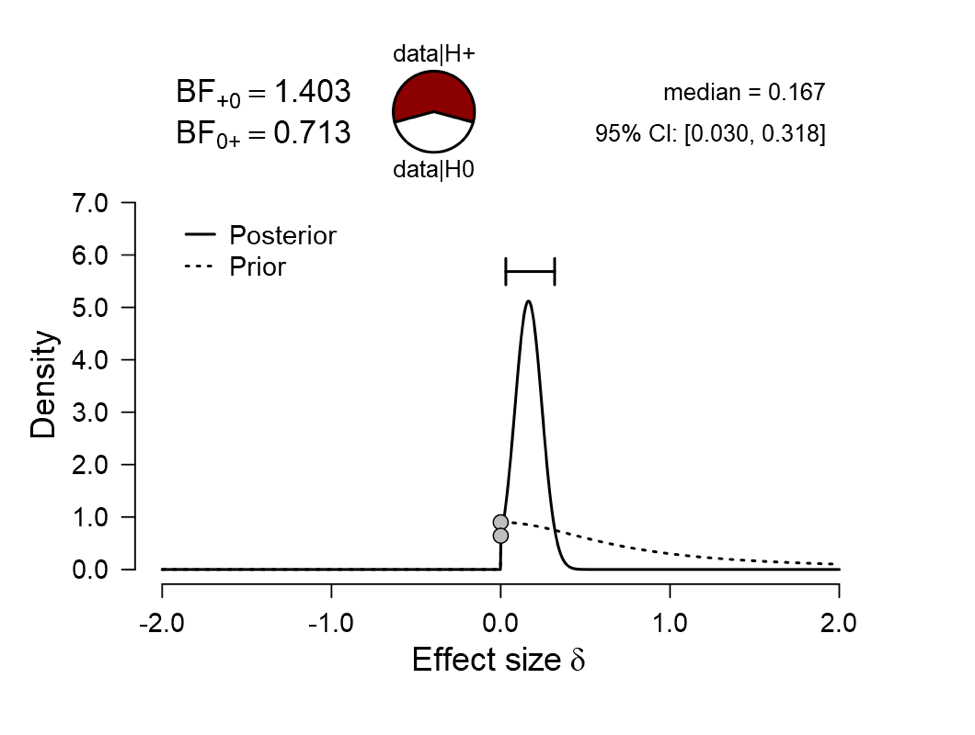
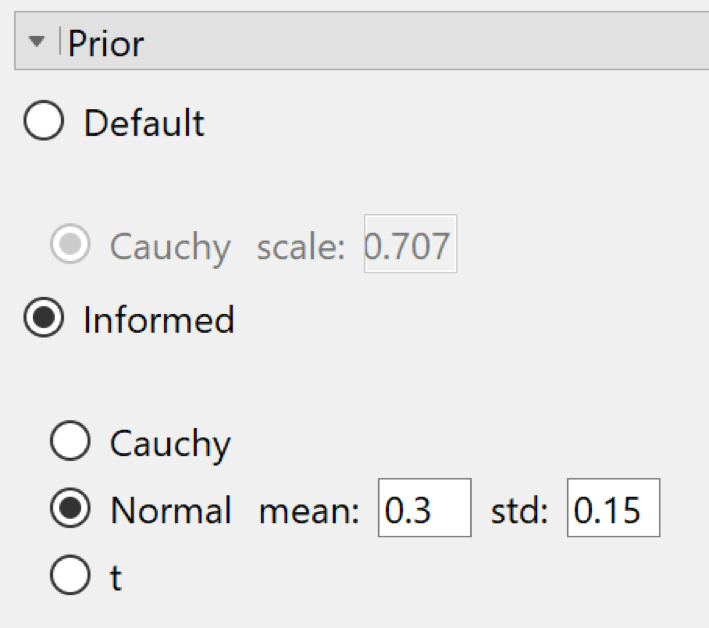
For our own multi-lab collaborative research effort on ego depletion, we preregistered an alternative hypothesis that assigns effect size a Gaussian prior distribution with mean 0.3 and standard deviation 0.15. This distribution is then truncated at zero, so that it only allows positive effect sizes. Such informed prior distributions (Gronau et al., 2017) can be specified in JASP under the “prior” submenu:
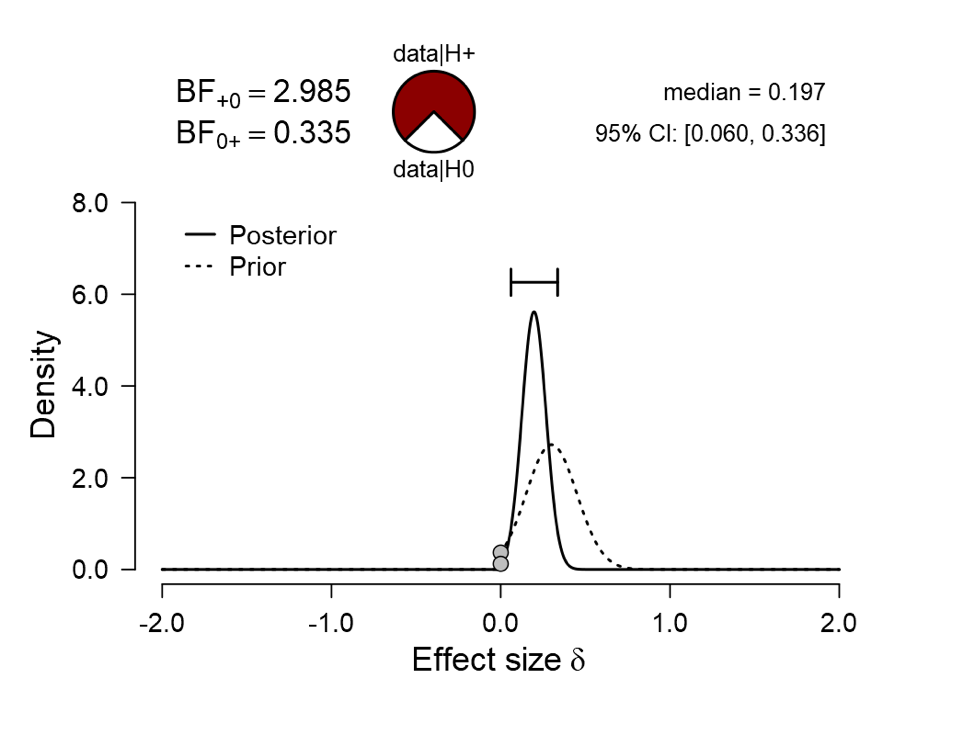
The result for the analysis with this informed prior is shown below:
For the informed analysis –which one may argue is the most appropriate for this specific case– the Bayes factor is almost 3.0. The pizza plot on top of the figure allows an intuitive assessment of how much evidence this represents; starting from a position of equal prior probability for H0 and H1, the posterior probability for H1 is 3/4 = 75%, leaving 25% for H0. This means that in the pizza plot, about one quarter is covered with mozzarella and three quarters are covered with pepperoni. Imagine poking your finger blindly into this pizza, and it comes back covered in mozzarella: how surprised are you? Not terribly surprised, it seems, and yet this is the level of evidence that corresponds to a p-just-below-.05 result.
Take-Home Message
- We have shown that –when it is actually calculated rather than intuited from the p-value alone– the evidence in Experiment 1 of the ego depletion preprint is not compelling, as the alternative hypothesis does not manage to convincingly outpredict the null hypothesis. Had the preregistered analysis of Experiment 2 also yielded a p-value just below .05, the combined result may have been more impressive; unfortunately, as detailed in the previous post, this was not the case.
- Despite testing an impressive number of participants, the evidence (for this particular dependent variable, and for this particular hypothesis) remains inconclusive. We did learn that, if the effect should exist, it is likely to be relatively small.
- We applied a wide range of priors, and found that the analysis that is arguably most appropriate (i.e., “Analysis III, the one-sided informed prior”) provided the strongest evidence against the null. Nevertheless, even the strongest evidence is not very strong, and considerable doubt remains.
- In JASP, the Bayesian analyses presented above take mere seconds to execute. We believe that these analyses promote a more inclusive and comprehensive perspective on statistical inference.
- There is certainly information in the data, but as far as evidence against the null hypothesis is concerned, the results are less strong than the p-value would lead one to believe. This constitutes yet another demonstration of how a sole focus on p-values can make well-intentioned researchers draw conclusions that are much stronger than are warranted by the data.
- A quick Bayesian reanalysis in JASP (or in the BayesFactor R package — Morey & Rouder, 2015) can protect researchers against the p-value induced overconfidence that continues to plague the field.
Like this post?
Subscribe to the JASP newsletter to receive regular updates about JASP including the latest Bayesian Spectacles blog posts! You can unsubscribe at any time.
References
Garrison, K. E., Finley, A. J., & Schmeichel, B. J. (2017). Ego depletion reduces attentional control: Evidence from two high-powered preregistered experiments. Manuscript submitted for publication. URL: https://psyarxiv.com/pgny3/.
Gronau, Q. F., Ly, A., & Wagenmakers, E.-J. (2017). Informed Bayesian t-tests. Manuscript submitted for publication. URL: https://arxiv.org/abs/1704.02479.
Ly, A., Verhagen, A. J., Wagenmakers, E.-J. (2016). Harold Jeffreys’s default Bayes factor hypothesis tests: Explanation, extension, and application in psychology. Journal of Mathematical Psychology, 72, 19-32.
Ly, A., Raj, A., Etz, A., Marsman, M., Gronau, Q. F., & Wagenmakers, E.-J. (2017). Bayesian reanalyses from summary statistics: A guide for academic consumers. Manuscript submitted for publication. URL: https://osf.io/7t2jd/.
Morey, R. D., & Rouder, J. N. (2015). BayesFactor 0.9.11-1. Comprehensive R Archive Network. URL: http://cran.r-project.org/web/packages/BayesFactor/index.html.
About The Authors

Eric-Jan Wagenmakers
Eric-Jan (EJ) Wagenmakers is professor at the Psychological Methods Group at the University of Amsterdam.

Quentin Gronau
Quentin is a PhD candidate at the Psychological Methods Group of the University of Amsterdam.