Geometric Intuition for a Surprising Result

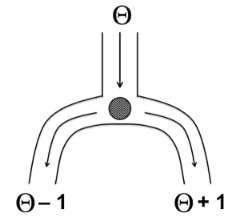
My colleague Raoul Grasman and I recently posted the preprint “A discrepancy measure based on expected posterior probability“. In this preprint, we show that the expected posterior probability for a true model Hf equals the expected posterior probability for a true alternative model Hg. It is not immediately obvious why this should be the case. In Appendix A of the…
read more