This week I came across an inspired/inspiring article by Jim Berger, “Learning statistics from counterexamples“. This short paper strikes at the very heart of statistics; it seems to me that every statistician (whether young or old, frequentist or Bayesian) ought to have an opinion on the counterexamples — sitting on the fence is not an option. Below I give the abstract and highlight one of 20 (!) counterexamples presented.

Berger’s Abstract

The title of this article is (essentially) the same as the famous paper Basu (2011b). Basu often opined that counterexamples were the best way to learn limitations of theories or methods and I have followed his directive in my own teaching. A number of counterexamples I use extensively in teaching are collected here. (Berger, in press)

Example of a Counterexample Featuring Confidence Intervals

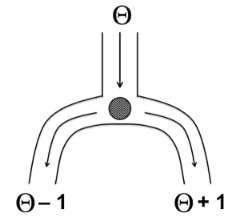
One counterexample discussed by Berger (Example 2) was presented earlier by Berger & Wolpert (1988), in a book whose contents is as terrific as the typesetting is terrible. I used this example myself in a later paper (Wagenmakers et al., 2018). The key idea can be visualized as follows:

Two balls are dropped consecutively in a tube at location 𝜃; each ball lands randomly at tube location 𝜃 − 1 or 𝜃 + 1. When the two balls land in different locations, 𝜃 is known with 100% certainty; when the two balls land in the same location, 𝜃 is known with 50% certainty. The pre-data average of 75% confidence is meaningless after the data have been observed. The example is taken from Berger & Wolpert (1988). (Wagenmakers et al., 2018, p. 41; see also Morey et al., 2016)

Key Reference

Berger, J. O. (in press). Learning statistics from counterexamples. Sankhya A.

Other References

Basu, D. (2011b). Learning statistics from counter examples: ancillary statistics. Selected Works of Debabrata Basu, pages 391–397.

Berger, J. O., & Wolpert, R. L. (1988). The likelihood principle, 2nd edn. Hayward (CA): Institute of Mathematical Statistics.

Morey, R. D., Hoekstra, R., Rouder, J. N., Lee, M. D., & Wagenmakers, E.-J. (2016). The fallacy of placing confidence in confidence intervals. Psychonomic Bulletin & Review, 23, 103-123.

Wagenmakers, E.-J., Marsman, M., Jamil, T., Ly, A., Verhagen, A. J., Love, J., Selker, R., Gronau, Q. F., Šmíra, M., Epskamp, S., Matzke, D., Rouder, J. N., Morey, R. D. (2018). Bayesian inference for psychology. Part I: Theoretical advantages and practical ramifications. Psychonomic Bulletin & Review, 25, 35-57.