WARNING: this post deals exclusively with a chess endgame study.

A previous post discussed the Bristol theme from chess endgame study composition. One of the featured studies was created by the great Leonid Kubbel. This is what I wrote:

“Since its inception, the Bristol theme has appealed to several composers. One of the most famous, Leonid Kubbel, created the following work of art:

After some foreplay that does not concern us here, the position in the diagram was reached. Black has a huge material advantage (queen and rook versus a lone bishop) but his pieces are boxed in and White has the terrible threat of transferring his bishop to h7 via e4, delivering checkmate. However, the Bristol theme comes to the rescue: 1… Ra1 tucks the rook into the corner, such that, after White initiates his intended manoeuvre 2. Be4 (threatening mate on h7), black counters with 2…Qb1!! Black offers the queen in order to prevent mate, a gift that White cannot accept, for after 3. Bxb1?? Rxb1 Black is a full rook to the good. (I mention this line because it shows that the Bristolian rook actually fulfills a function in this study, namely to defend the queen once it has arrived on b1) Suddenly it looks as if Black is completely winning. In dire straits, White comes up with a miraculous save: 3. Bf5!!, offering White’s only remaining piece. Black has no choice but to accept, yet after 3…Qxf5 the results is stalemate, and consequently a draw.

As an aside, Tim Krabbe mentions a dual: “PS 1 June 2004: As Steve Grant remarks, 1…Rg1 very likely doesn’t win either: 2.Be4 Rg6+ 3.Bxg6 fxg6 4.f7+ Kxf7 5.Kh7 etc.” [paraphrased] The machine evaluates this as +0.8, a slight advantage to white, but probably not enough to win.

As it turns out, quite a lot of what I wrote is inaccurate at best. First, the assignment of the study was “White to play and draw”; hence, the prosaic 1…Rg1 does not qualify as a dual. Second, when I looked at this more carefully, it turns out that after Grant’s 1…Rg1 2. Be4 Rg6+ 3. Bxg6 black can immediately draw with the pretty 3…Qb1! rather than acquiesce to a lengthy torture in a slightly worse queen endgame.

Nevertheless, when I was still under the impression that 1…Rg1 was a serious flaw, I decided to try and “fix” the study. To begin with, I looked up the study’s description in Herbstman’s fabulous 1943 book. In the margin to the study, I had written, about 25 years ago (!): “Black does not need to play 3…Qf5 and stalemate the white king. Instead, Black can play 3…Ra5!? 6. Bxb1 Rh5+ (as an aside, 6…Rf5 Lxf5 stalemate is also pretty) 7. Kxh5 and Black has produced a self-stalemate.” The fact that Black can choose to stalemate White or be stalemated himself is amusing. There does not appear to be an official term for this motiv, which may be relatively rare. At any rate, I was pleased with myself for discovering the option 3…Ra5: finding such a move requires persistence, creativity, and the capacity for independent thought. My enthusiasm was considerably lessened, however, when I noticed that the margin text credited my old study-solving buddy IM Eelke Wiersma with this insight. So: well done, Eelke!

However, I was still unhappy with the Kubbel study. In particular, I disliked the idea that Black could play 1…Rg1 and then opt for Grant’s worse endgame. What I wanted is to change the study so that the 3…Qb1! resource is absolutely required to hold the draw. In the end, after some computer-assisted tinkering, this is what I came up with (I provide the study in its entirety this time):

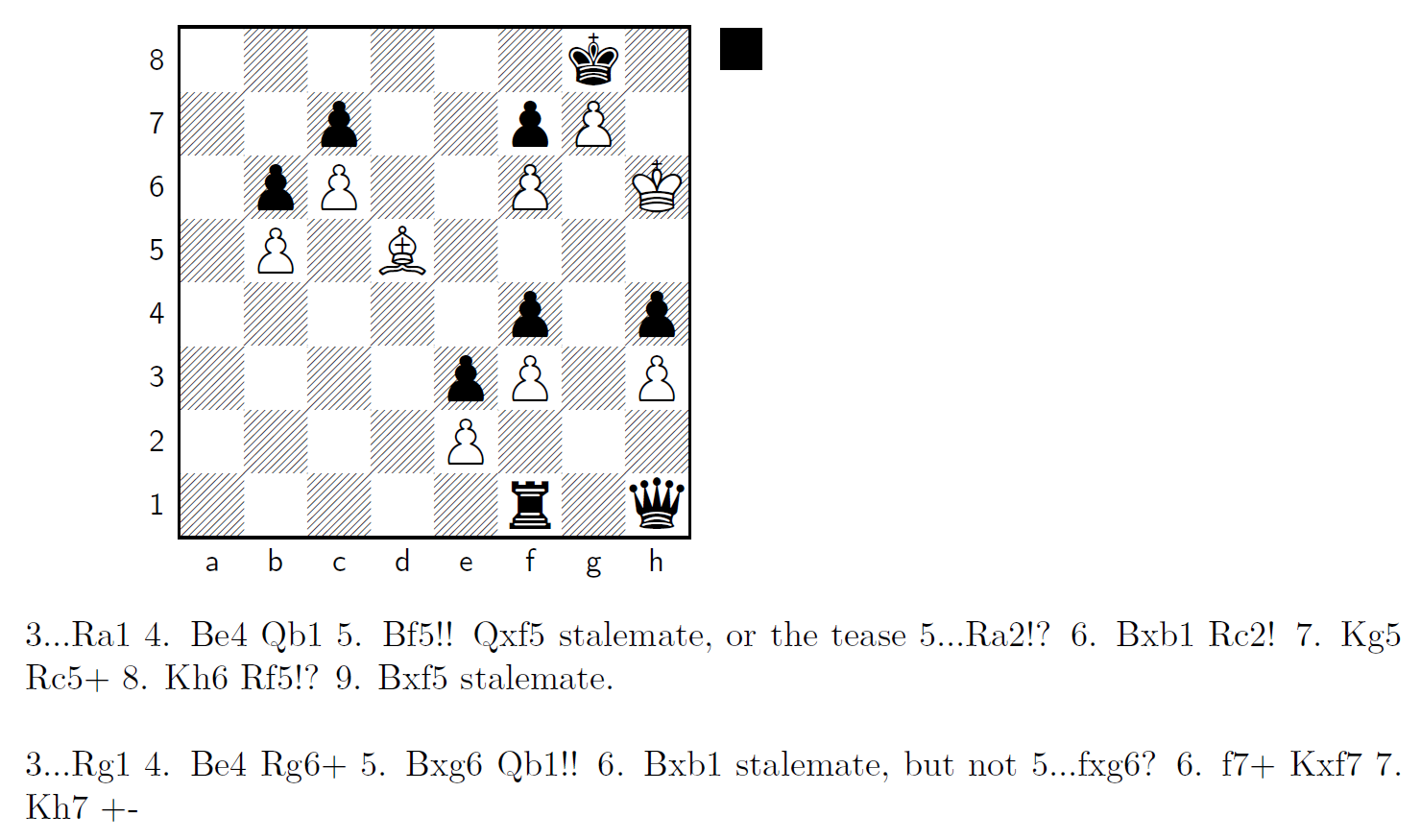
Of course this is not a major improvement on the original, but it seems to me that it is some small improvement nonetheless. Regardless, one can only marvel at the ingenuity and brilliance of Leonid Kubbel, who had to construct studies without the assistance of a computer.

References

Herbstman, A. O. (1943). De schaakstudie in onze dagen [the modern-day chess study]. Lochem: de Tijdstroom.

About The Author

Eric-Jan Wagenmakers

Eric-Jan (EJ) Wagenmakers is professor at the Psychological Methods Group at the University of Amsterdam.