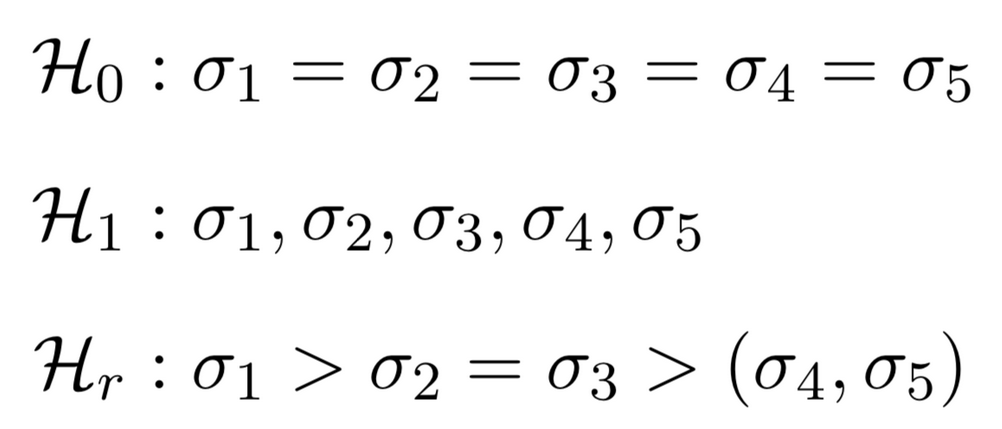Corona and the Statistics Wars

As the corona-crisis engulfs the world, politicians left and right are accused of “politicizing” the pandemic. In order to follow suit I will try to weaponize the pandemic to argue in favor of Bayesian inference over frequentist inference. In recent months it has become clear that the corona pandemic is not just fought by doctors, nurses, and entire populations as…
read more