In a recent blog post, Bayesian icon David Spiegelhalter proposes a new analysis of the results from the ANDROMEDA-SHOCK randomized clinical trial. This trial was published in JAMA under the informative title “Effect of a Resuscitation Strategy Targeting Peripheral Perfusion Status vs Serum Lactate Levels on 28-Day Mortality Among Patients With Septic Shock”.

In JAMA, the authors summarize their findings as follows: “In this randomized clinical trial of 424 patients with early septic shock, 28-day mortality was 34.9% [74/212 patients] in the peripheral perfusion–targeted resuscitation [henceforth PPTR] group compared with 43.4% [92/212] in the lactate level–targeted resuscitation group, a difference that did not reach statistical significance.” The authors conclude that “These findings do not support the use of a peripheral perfusion–targeted resuscitation strategy in patients with septic shock.”

Spiegelhalter rightly complained that this all-or-none conclusion in JAMA seems at odds with the presence of a 8.5% benefit of PPTR in the sample:

“I remain highly critical of the conclusion expressed in JAMA that there was ‘no effect’ based on a two-sided P-value of 0.06, incidentally corresponding to a P-value of 0.03 for the alternative one-sided alternative hypothesis that the treatment improved. But note that I did not at any time suggest that there was clear benefit.”

How then should these data be analyzed, and what conclusion is reasonable? Spiegelhalter provides a Bayesian perspective, one that we believe warrants some critical reflection. Spiegelhalter starts:

“So what Bayesian view might be reasonable? First, a rather naive uniform prior on the log-hazard ratio would lead to a 97% posterior probability that the new treatment was beneficial, which might even be interpreted as ‘clear benefit’. But, as H&I correctly point out, there is a long history of failed innovations in this context, and a substantial degree of scepticism is appropriate.”

Immediately we have to be on our guard. As Dennis Lindley was wont to point out, the Bayesian world is relative, and it is good to be keenly aware of what alternatives are being considered. Here, there is 97% posterior probability that the new treatment was beneficial. The remaining 3% is the posterior probability that the new treatment is actually harmful. Do these posterior probabilities address the researchers’ key question? We very
much doubt it. What the researchers wanted to demonstrate is that the new treatment outperforms the standard, and the most intuitive comparison is to the idealized position of a hard-nosed skeptic, who would argue that the effect is either absent or so small as to be irrelevant. This skeptic would not propose that the new treatment is actually harmful — this yields risky predictions that are unlikely to hold true. In general, it is much easier to demonstrate that an effect is helpful rather than harmful than it is to demonstrate that an effect is helpful rather than ineffective. And it is the latter demonstration that is needed to convince the medical field to change the status quo. Bottom-line: the 97% posterior probability of a benefit is less relevant than it appears at first sight.

Spiegelhalter continues:

“One way of incorporating such scepticism is to use a prior with a ‘spike’ on ‘no effect’, and a distribution over potential effects were this ‘null hypothesis’ false, which leads naturally to a Bayes factor approach. But since every treatment must have some effect on average, if only minor and of no clinical importance, my preference is to use a continuous prior, centred on ‘no effect’, and expressing scepticism about substantial treatment effects.”

In our opinion, this line of reasoning is as common as it is peculiar. Spiegelhalter notes that the null hypothesis is never true exactly (as many have done before him, and many will continue to do after him). Based on this claim, he then discards the testing framework altogether and embraces an estimation framework instead. This is a dramatic change of course based on a concern that can easily be accommodated. If the objection to the point-null hypothesis is that “every treatment must have some non-zero effect, no matter how miniscule”, then why not address this objection head-on and replace the point-null hypothesis with a peri-null hypothesis, one that assigns effect size a distribution that is tightly centered around zero? Not only does this eliminate the theoretical concern about the falsity of the point-null hypothesis, but practical application will reveal that the Bayes factor involving the point-null will usually be very, very close to the Bayes factor involving the peri-null hypothesis. Here is an analogy: suppose you are interested in buying a house with a lawn, but upon inspection you discover that the grass has grown rather high. This observation would not prompt you to abandon the transaction and start looking at apartments in high-rise buildings instead. Most reasonable people would just buy the house and mow the lawn.

After completely discarding the skeptic’s point-null or peri-null hypothesis, Spiegelhalter continues and estimates the posterior probability that the new treatment is beneficial (instead of harmful!) using a prior distribution that is fairly peaked around the null value. Spiegelhalter then concludes “This sceptical prior would lead to a posterior probability of 92% that the treatment reduced average mortality”. As before, it is prudent to notice that the remaining 8% goes to the proposition that the new treatment increases average mortality. And as before, this may not correspond to the question of interest. Also, note that the posterior probability of 92% is only a little less than that of 97%; Spiegelhalter’s skeptical prior is quickly overwhelmed by the data. A hard-nosed skeptic will find it unappealing that a few hundred binary observations suffice to wash out most initial doubts about treatment efficacy. Spiegelhalter’s skeptic appears to be relatively gullible, because she accepts, right off the bat, that the treatment effect is (1) definitely not zero; (2) just as likely to be helpful as harmful.

A Bayes Factor Re-analysis Featuring a Hard-Nosed Skeptic

Here we briefly consider a Bayes factor re-analysis of the ANDROMEDA-SHOCK data. For simplicity, we use a standard test for the equality of two proportions (Kass & Vaidyanathan, 1992 — henceforth “KV”). The KV test is a Bayesian logistic regression with “condition” (i.e., treatment vs. control) coded as a dummy predictor. The KV test has been implemented in the R package abtest (Gronau et al., 2019), and is also available in JASP.

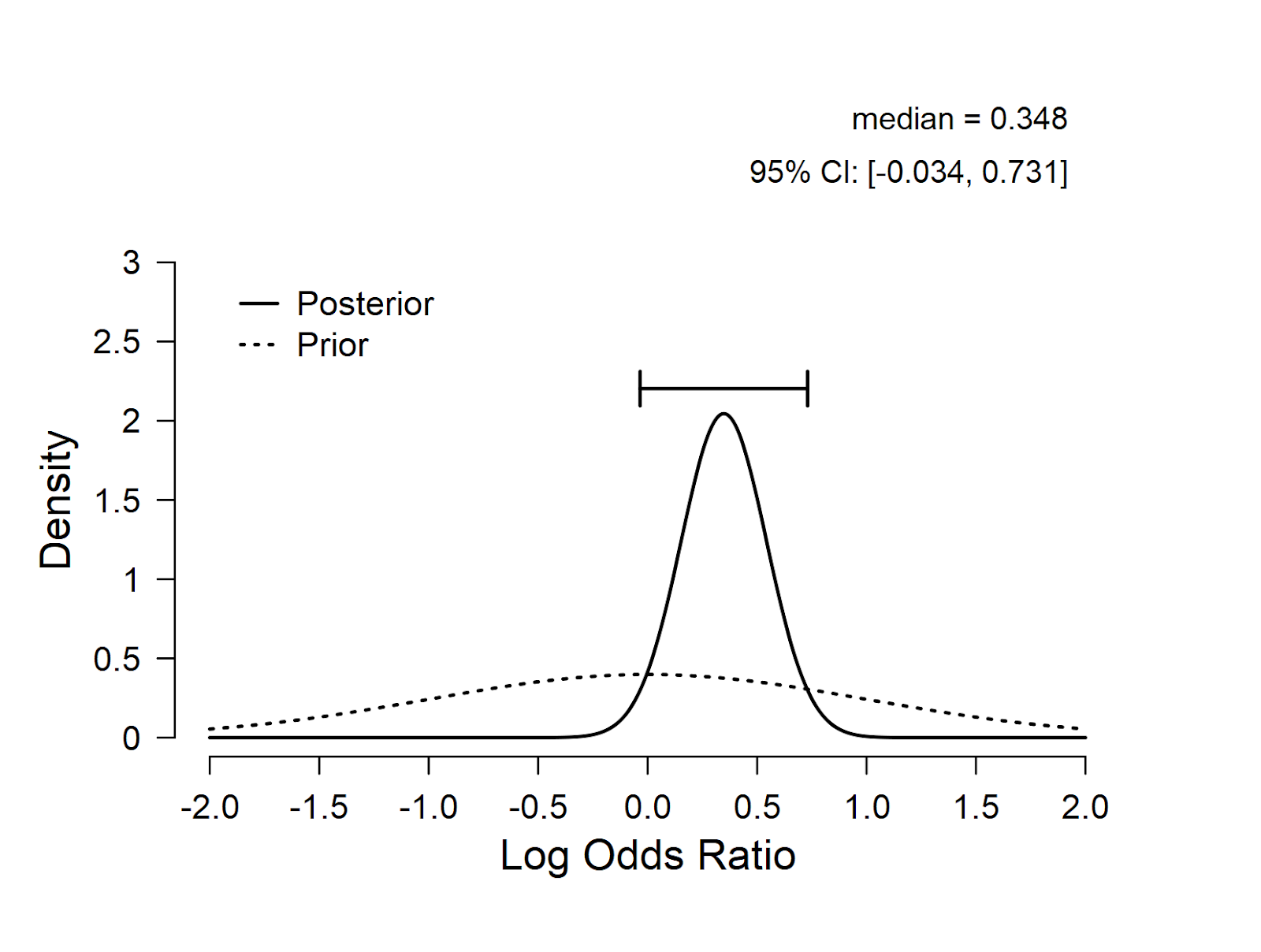
Below we use our default standard normal prior on the test-relevant parameter, which is the log odds ratio. The prior and posterior distribution for the log odds ratio are shown in the figure. The log odds ratio has a posterior median of 0.348, with most mass on positive values. This suggests that the new treatment is likely to be helpful rather than harmful.

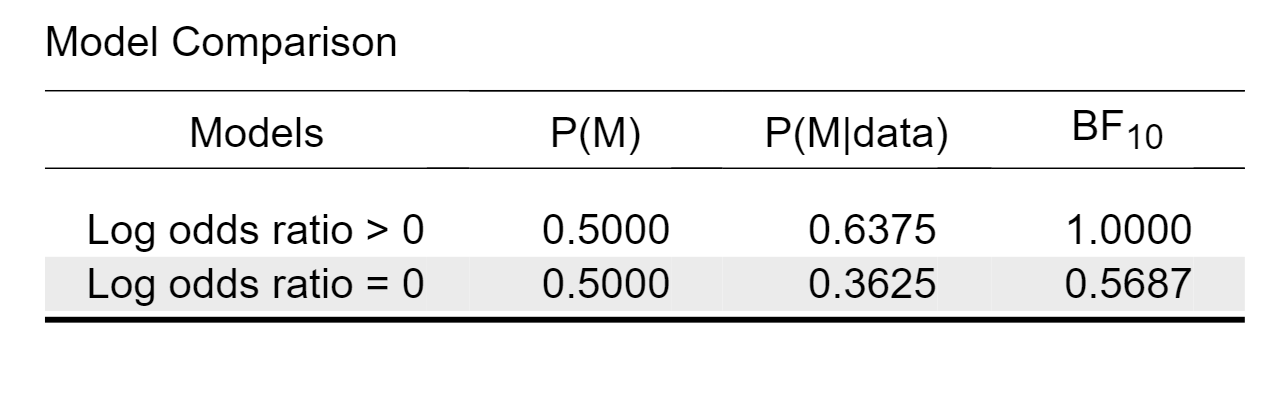
When we use a testing framework our default setting is to compare three hypotheses: (1) the treatment is ineffective (i.e., log odds ratio = 0; the idealized position of a hard-nosed skeptic); the treatment is helpful (i.e., log odds ratio > 0) and (3) the treatment is harmful (i.e., log odds ratio < 0). The resulting table output in JASP is here:

This table shows that the model that predicts the data best states that the treatment is helpful; compared to the null model, the Bayes factor is 1.83, meaning that the data are almost twice as likely under the hypothesis that the treatment helps. This level of evidence, however, is only weak. In JASP we can easily change the prior probabilities for the models, and here we will assign the two relevant models equal probability. The resulting table is here:

So, when both models are deemed equally like a priori, a Bayes factor of 1.8 raises the model probability from 50% to about 64%, leaving about 36% for the null hypothesis. This level of evidence represents “absence of evidence” more than it does “evidence of absence”. In the terminology of Harold Jeffreys, the evidence is “not worth more than a bare mention”. In other words, our analysis is consistent with Spiegelhalter’s general assessment: the data support the hypothesis that the treatment is effective, but not in a compelling fashion. We simply need more data. As an aside, it appears that the null hypothesis, despite being “always false”, does not perform badly at all in terms of prediction.

From the first table it is also possible to compute, by transitivity, the evidence for the hypothesis that the treatment is helpful rather than harmful. Specifically, the associated Bayes factor is 1.8348/0.0712 = 25.77. In other words, there is good evidence that the treatment is helpful rather than harmful, but at the same time there is only weak evidence that the treatment is helpful rather than ineffective. In order to draw stronger conclusions more data need to be collected.

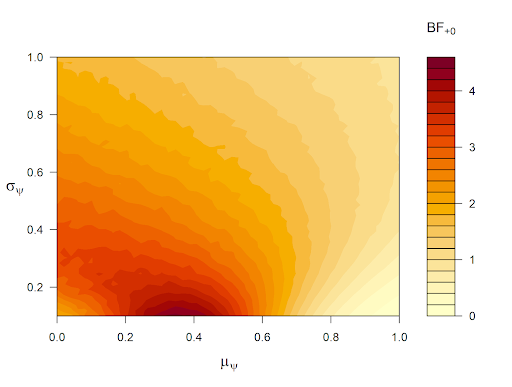
It is of course possible to adjust the above analysis, either by replacing the hard-nosed point-null hypothesis with a peri-null hypothesis, or by changing the prior distribution on the log odds ratio from a standard normal to something else. In the upcoming JASP version, we have implemented a robustness analysis (already available in the R package abtest), where we can see how much the Bayes factor changes as a function of mu and sigma (where the log odds ratio ~ N(mu, sigma)). Below is a heatmap of Bayes factors produced by varying mu from 0 to 1 and sigma from 0.1 to 1. The legend next to the heatmap already suggests that the evidence in favor of a treatment benefit (versus treatman ineffectiveness) is never compelling, regardless of the prior distribution that is set. The Bayes factor is highest when mu is near the maximum likelihood estimate in the sample and sigma is small. But even this oracle prior, which is cherry-picked to produce compelling evidence for a treatment benefit, does not yield a result that should suffice to alter medical practice. Note that a Bayes factor of 4 changes a prior probability of 0.50 to 0.80, leaving 20% for the null hypothesis.

In sum, our reanalysis shows that the data contradict the JAMA authors’ conclusion that “These findings do not support the use of a peripheral perfusion–targeted resuscitation strategy in patients with septic shock.” The data do support PPTR, but not to a degree that suffices to convince a skeptic (or the medical community). This conclusion is qualitatively in line with that of David Spiegelhalter, although we of course prefer our own analysis. 🙂

References

Smith, A. F. M., & Spiegelhalter, D. J. (1980). Bayes factors and choice criteria for linear models. Journal of the Royal Statistical Society B, 42, 213-220.

About The Authors

Eric-Jan Wagenmakers

Eric-Jan (EJ) Wagenmakers is professor at the Psychological Methods Group at the University of Amsterdam.

Quentin F. Gronau

Quentin is a PhD candidate at the Psychological Methods Group of the University of Amsterdam.