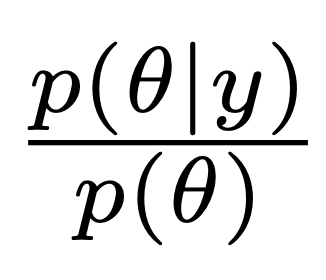The Misconception
The relative belief ratio (e.g., Evans 2015, Horwich 1982/2016) equals the marginal likelihood.
The Correction
The relative belief ratio is proportional to the marginal likelihood. Dividing two marginal likelihoods (i.e., computing a Bayes factor) cancels the constant of proportionality, such that the Bayes factor equals the ratio of two complementary relative belief ratios (Evans 2015, p.109, proposition 4.3.1).
The Explanation
In the highly recommended book Measuring statistical evidence using relative belief, Evans (2015) defines evidence as follows (see also Carnap 1950, pp. 326-333; Horwich 1982/2016, p. 48; Keynes 1921, p. 170):
where ![]() represents a parameter (or, more generally, a model, a hypothesis, a claim, or a proposition). In other words, data provide evidence for a claim
represents a parameter (or, more generally, a model, a hypothesis, a claim, or a proposition). In other words, data provide evidence for a claim ![]() to the extent that they make
to the extent that they make ![]() more likely than it was before. This is a sensible axiom; who would be willing to argue that data provide evidence for a claim when they make that claim less plausible than it was before?
more likely than it was before. This is a sensible axiom; who would be willing to argue that data provide evidence for a claim when they make that claim less plausible than it was before?
Evans formulates the Principle of Evidence as follows: “If ![]() , then there is evidence in favor of
, then there is evidence in favor of ![]() being true because the belief in
being true because the belief in ![]() has increased. If
has increased. If ![]() , then there is evidence against
, then there is evidence against ![]() being true because the belief in
being true because the belief in ![]() has decreased. If
has decreased. If ![]() , then there is neither evidence in favor of
, then there is neither evidence in favor of ![]() nor against
nor against ![]() because the belief in
because the belief in ![]() has not changed.” (Evans 2015, p. 96). For concreteness, consider the scenario where we entertain only two models,
has not changed.” (Evans 2015, p. 96). For concreteness, consider the scenario where we entertain only two models, ![]() and
and ![]() . The relative belief ratio (RB) for
. The relative belief ratio (RB) for ![]() is
is
and the relative belief ratio for ![]() is
is
Here we examine how the RB is related to the marginal likelihood and the Bayes factor. The Bayes factor quantifies the extent to which the data warrant an update from prior to posterior model odds:
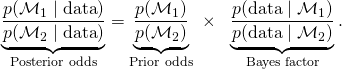
The above equation shows that the Bayes factor is also the ratio of two marginal likelihoods, that is, the relative predictive adequacy for the observed data under the rival models. When the Bayes factor ![]() is larger than 1,
is larger than 1, ![]() outpredicts
outpredicts ![]() ; when
; when ![]() is smaller than 1,
is smaller than 1, ![]() outpredicts
outpredicts ![]() ; and when
; and when ![]() equals 1,
equals 1, ![]() and
and ![]() predict the data equally well. To see the relation with the RB, we may rearrange the above equation as follows (Evans 2015, p. 109, proposition 4.3.1):
predict the data equally well. To see the relation with the RB, we may rearrange the above equation as follows (Evans 2015, p. 109, proposition 4.3.1):
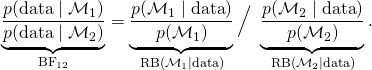 (1)
(1)In words, the Bayes factor is the ratio between the two relative belief ratios for the competing models. When only two models are in play, the probabilities involving ![]() can be rewritten as the complement of
can be rewritten as the complement of ![]() , and the Bayes factor may be interpreted as a scaling operation on the relative belief ratio.
, and the Bayes factor may be interpreted as a scaling operation on the relative belief ratio.
But now we have
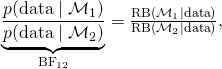
and this invites the interpretation that the marginal likelihood under model ![]() , that is,
, that is, ![]() , equals the relative belief ratio for that model,
, equals the relative belief ratio for that model, ![]() . That this interpretation is false is evident from a simple counterexample. Consider two data sets, one large and one small, that yield the exact same
. That this interpretation is false is evident from a simple counterexample. Consider two data sets, one large and one small, that yield the exact same ![]() ; these data sets necessitate the same adjustment in beliefs, and therefore produce the same relative belief ratios
; these data sets necessitate the same adjustment in beliefs, and therefore produce the same relative belief ratios ![]() and
and ![]() . However, the marginal likelihood for the large data set will usually be much lower than that of the small data set. Thus, we have that
. However, the marginal likelihood for the large data set will usually be much lower than that of the small data set. Thus, we have that ![]() , where the constant of proportionality is the same for
, where the constant of proportionality is the same for ![]() and
and ![]() .
.
Remark 1
When the two components of the relative belief ratio are known, the Bayes factor is determined as per Equation 1; However, when the two components of the Bayes factor are known (i.e., the marginal likelihoods of the two rival models), this does not determine the separate relative belief ratios; the relative belief ratios depend on the prior model probabilities, whereas the Bayes factor considers only the models’ relative predictive performance.
Remark 2
The Bayes factor accords with Evans’ Principle of Evidence. Suppose that ![]() ; then
; then ![]() , and both RBs in Equation 1 evaluate to 1 such that
, and both RBs in Equation 1 evaluate to 1 such that ![]() also. Further, suppose that
also. Further, suppose that ![]() ; then
; then ![]() , and consequently
, and consequently ![]() , so
, so ![]() .
.
Remark 3
Evans (2015, p. 109, proposition 4.3.1) also provides the following identity:
Using this identity, it is straightforward to demonstrate that the relative belief ratio and the Bayes factor may order evidence differently. For instance, consider two scenarios. In scenario A we have ![]() , and in scenario B we have
, and in scenario B we have ![]() . In both scenarios model
. In both scenarios model ![]() outpredicts
outpredicts ![]() , but the difference in predictive performance is largest in scenario A. From the perspective of Bayes factors, scenario A yields stronger evidence in favor of
, but the difference in predictive performance is largest in scenario A. From the perspective of Bayes factors, scenario A yields stronger evidence in favor of ![]() than does scenario B. Consider now that in scenario A, we have
than does scenario B. Consider now that in scenario A, we have ![]() , that is,
, that is, ![]() is more plausible a priori than
is more plausible a priori than ![]() . As per Equation 2, the associated relative belief ratio is
. As per Equation 2, the associated relative belief ratio is ![]() . In scenario B, assume we have
. In scenario B, assume we have ![]() , that is,
, that is, ![]() is less plausible a priori than
is less plausible a priori than ![]() . The associated relative belief ratio is
. The associated relative belief ratio is ![]() . From the perspective of relative belief ratios, scenario B yields stronger evidence for
. From the perspective of relative belief ratios, scenario B yields stronger evidence for ![]() than does scenario A — a reversal from the ordering given by the Bayes factor!
than does scenario A — a reversal from the ordering given by the Bayes factor!
Remark 4
Assume ![]() . If
. If ![]() , then
, then ![]() ; if
; if ![]() , then
, then ![]() ; finally, if
; finally, if ![]() , then
, then ![]() . These three relative belief ratios (
. These three relative belief ratios (![]() ,
, ![]() ,
, ![]() ) are numerically close, and may suggest that the evidence is of similar strength. In contrast, the respective Bayes factors are
) are numerically close, and may suggest that the evidence is of similar strength. In contrast, the respective Bayes factors are ![]() ,
, ![]() , and
, and ![]() — each one differs from its predecessor by an order of magnitude. More dramatically still, suppose
— each one differs from its predecessor by an order of magnitude. More dramatically still, suppose ![]() holds ‘not all zombies are hungry’ whereas
holds ‘not all zombies are hungry’ whereas ![]() holds ‘all zombies are hungry’. A satiated zombie is observed. With
holds ‘all zombies are hungry’. A satiated zombie is observed. With ![]() , the relative belief ratio
, the relative belief ratio ![]() . The Bayes factor in favor of
. The Bayes factor in favor of ![]() , in contrast, is infinity — the observation that occurred was deemed impossible under
, in contrast, is infinity — the observation that occurred was deemed impossible under ![]() , so this model is `irrevocably exploded’ by the data (Polya, 1954).
, so this model is `irrevocably exploded’ by the data (Polya, 1954).
Remark 5
The Bayes factor assesses evidence by quantifying relative predictive performance, which depends solely on the marginal likelihood and is unaffected by the prior model probabilities. In contrast, the relative belief ratio involves the prior model probability as a crucial component.
Remark 6
There is a special case where the relative belief ratio does correspond to a Bayes factor. This case arises when there exists a single overarching `encompassing’ model, ![]() , and it is of interest to quantify the degree to which the data provide support for a restriction of that model’s parameter space.
, and it is of interest to quantify the degree to which the data provide support for a restriction of that model’s parameter space.
For concreteness, let ![]() denote the encompassing model under which the prior distribution for a binomial parameter
denote the encompassing model under which the prior distribution for a binomial parameter ![]() is assigned a uniform distribution:
is assigned a uniform distribution: ![]() . We consider two complementary restrictions on
. We consider two complementary restrictions on ![]() : model
: model ![]() states that
states that ![]() is smaller than some arbitrary threshold value
is smaller than some arbitrary threshold value ![]() , that is,
, that is, ![]() , whereas model
, whereas model ![]() states that
states that ![]() is larger than
is larger than ![]() , that is,
, that is, ![]() . In the following, we denote
. In the following, we denote ![]() by
by ![]() .
.
Klugkist et al. (2005a) have shown that, for the test of a parameter restriction of an encompassing model, the Bayes factor equals the relative belief ratio:
In words, the Bayes factor for the restricted model ![]() versus the encompassing model
versus the encompassing model ![]() equals the change from prior to posterior mass under
equals the change from prior to posterior mass under ![]() in line with the restriction proposed by
in line with the restriction proposed by ![]() . When the interval shrinks to a point, this relative belief ratio becomes the ‘Savage-Dickey density ratio test’, that allows the Bayes factor for a point hypothesis to be computed as the ratio of ordinates for the prior and posterior distribution under
. When the interval shrinks to a point, this relative belief ratio becomes the ‘Savage-Dickey density ratio test’, that allows the Bayes factor for a point hypothesis to be computed as the ratio of ordinates for the prior and posterior distribution under ![]() evaluated at the value proposed under
evaluated at the value proposed under ![]() (e.g., Wetzels et al. 2010).
(e.g., Wetzels et al. 2010).
In the binomial scenario above, assume that virtually all posterior mass is lower than, say, ![]() . Then
. Then ![]() is approximately
is approximately ![]() , the maximum possible support for
, the maximum possible support for ![]() versus
versus ![]() . It should be stressed that this `encompassing Bayes factor’ compares predictive performance of
. It should be stressed that this `encompassing Bayes factor’ compares predictive performance of ![]() to that of the encompassing model
to that of the encompassing model ![]() , and it is therefore a test using an overlapping hypothesis. However, from this we can easily construct a test for non-overlapping or ‘dividing’ hypotheses as follows.
, and it is therefore a test using an overlapping hypothesis. However, from this we can easily construct a test for non-overlapping or ‘dividing’ hypotheses as follows.
First we state the complementary relative belief ratio, that is, the Bayes factor for the opposite-restricted model ![]() versus the encompassing model
versus the encompassing model ![]() :
:
We then obtain the Bayes factor for the non-overlapping models ![]() versus
versus ![]() by dividing the two relative belief ratios:
by dividing the two relative belief ratios:
which can of course be rewritten in the standard form, as a change from prior to posterior odds:
References
Carnap, R. (1950). Logical Foundations of Probability. The University ofChicago Press, Chicago.
Evans, M. (2015). Measuring Statistical Evidence Using Relative Belief. CRCPress, Boca Raton, FL.
Horwich, P. (1982/2016). Probability and Evidence. Cambridge University Press, Cambridge.
Keynes, J. M. (1921). A Treatise on Probability. Macmillan & Co, London.
Klugkist, I. ,Laudy, O. , and Hoijtink, H. (2005a). Inequality constrainedanalysis of variance: A Bayesian approach. Psychological Methods, 10:477–493.
Polya, G. (1954). Mathematics and Plausible Reasoning: Vol. I. Induction and Analogy in Mathematics. Princeton University Press, Princeton, NJ.
Wetzels, R. , Grasman, R. P. P. P. , and Wagenmakers, E.-J. (2010). An encom-passing prior generalization of the Savage–Dickey density ratio test. Computational Statistics & Data Analysis, 54:2094–2102.
About The Authors

Eric-Jan Wagenmakers
Eric-Jan (EJ) Wagenmakers is professor at the Psychological Methods Group at the University of Amsterdam.

Quentin F. Gronau
Quentin is a PhD candidate at the Psychological Methods Group of the University of Amsterdam.