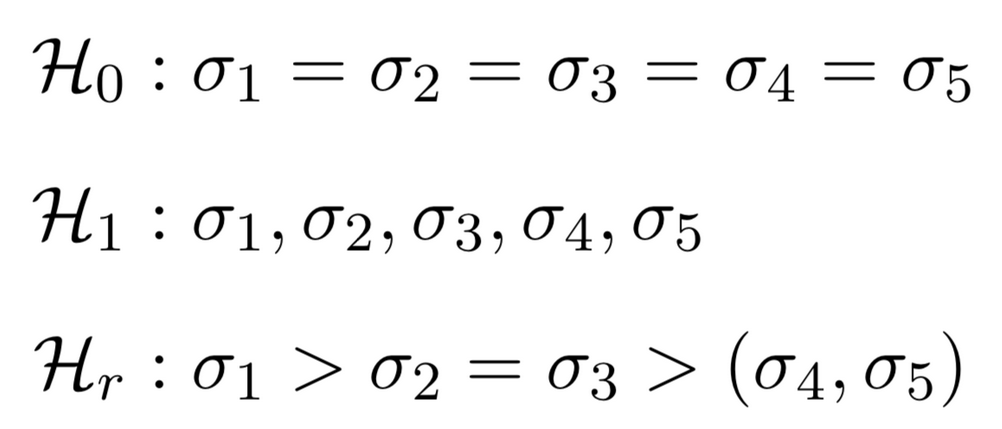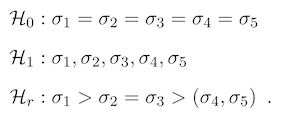Preprint: Default Bayes Factors for Testing the (In)equality of Several Population Variances

This post summarizes Dablander, F.⭑, van den Berg, D.⭑, Ly, A., Wagenmakers, E.-J. (2020). Default Bayes Factors for Testing the (In)equality of Several Population Variances. Preprint available on ArXiv:                                     https://arxiv.org/abs/2003.06278.

Abstract

“Testing the (in)equality of variances is an important problem in many statistical applications. We develop default Bayes factor tests to assess the (in)equality of two or more population variances, as well as a test for whether the population variance equals a specific value. The resulting test can be used to check assumptions for commonly used procedures such as the t-test or ANOVA, or test substantive hypotheses concerning variances directly. We further extend the Bayes factor to allow H0 to have a null-region. Researchers may have directed hypotheses such as \sigma^2_1 > \sigma^2_2, or want to combine hypotheses about equality with hypotheses about inequality, for example \sigma^2_1 = \sigma^2_2 > (\sigma^2_3, \sigma^2_4). We generalize our Bayes factor to accommodate such hypotheses for K > 2 groups. We show that our Bayes factor fulfills a number of desiderata, provide practical examples illustrating the method, and compare it to a recently proposed fractional Bayes factor procedure by Böing-Messing and Mulder (2018). Our procedure is implemented in the R package bfvartest.”

Motivation

“Testing the (in)equality of variances is important in many sciences and applied contexts. In engineering, for example, researchers may want to assess whether a new, cheaper measure- ment instrument achieves the same precision as the gold standard (Sholts, Flores, Walker, & Wärmländer, 2011). In genetics and medicine, scientists are not only interested in studying the genetic effect on the mean of a quantitative trait, but also on its variance (Paré, Cook, Ridker, & Chasman, 2010). In economics and archeology, ideas such as that increased economic pro- duction should reduce variability in products directly lead to statistical hypotheses on variances (Kvamme, Stark, & Longacre, 1996). In a court of law, one may be interested in reducing unwanted variability in civil damage awards and may want to compare how different interven- tions reduce this variability (Saks, Hollinger, Wissler, Evans, & Hart, 1997). In psychology, educational researchers may be interested in studying how the variance in pupil’s mathematical ability changes across school grades (Aunola, Leskinen, Lerkkanen, & Nurmi, 2004).”

Highlights

Our default Bayes factor fulfills a number of desiderata (measurement invariance, model selection consistency, information consistency, etc.) and generalizes a recently proposed automatic fractional Bayes factor (Böing-Messing & Mulder, 2018). We provide a one-sample and two-sample test for which researchers can elicit informative prior distributions, as well as conduct a sensitivity analysis. We generalize the Bayes factor to K > 2 groups and allow testing of ‘mixed’ or ‘informative’ hypotheses of the form:

This allows researchers to straightforwardly translate their substantive hypotheses on standard deviations / variances into statistical hypotheses, something that is not possible with classical p-value testing.

Examples

We provide a number of examples from engineering, paleoanthropology, personality psychology, archeology, and educational psychology. Below is the simple R code to reproduce part of the examples from psychology. Check out the paper and Github repository for more!
 

devtools::install_github(
    'fdabl/bfvartest',
    build_vignettes = TRUE
)
library('bfvartest')

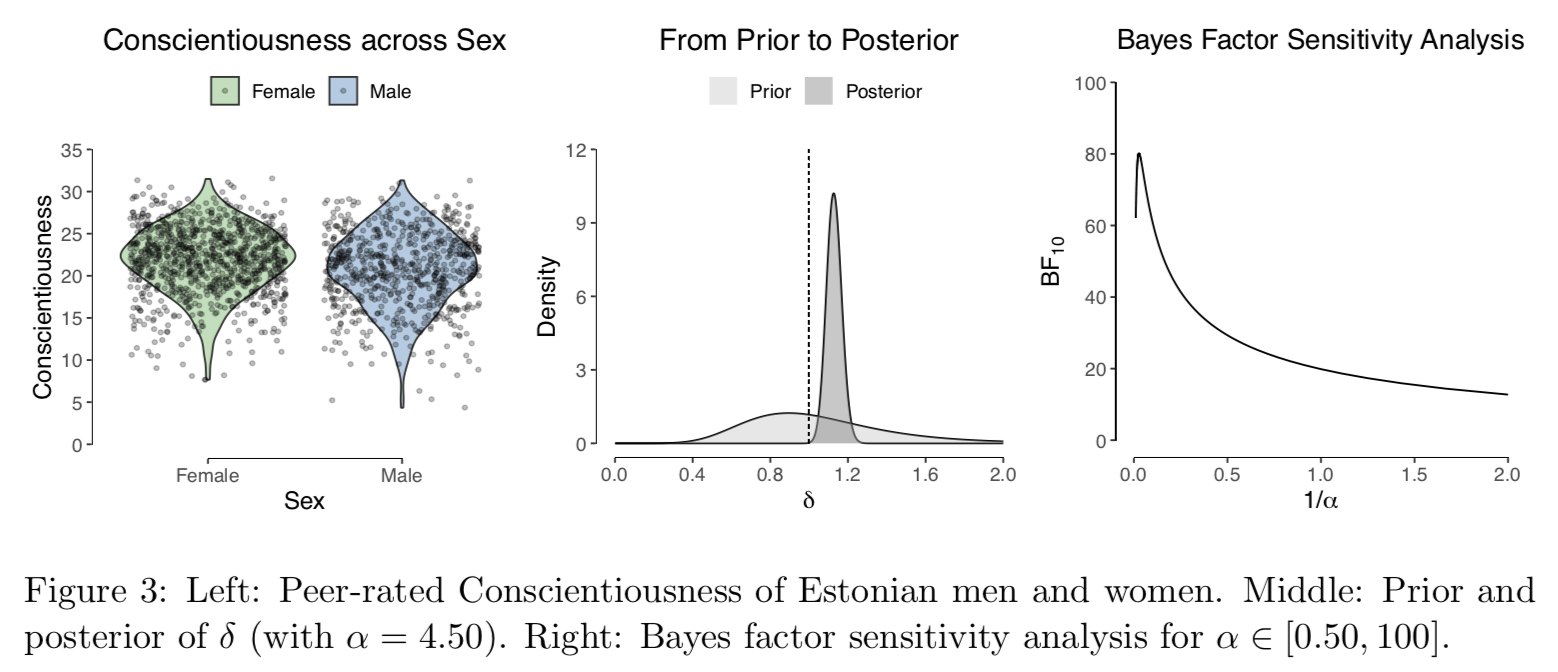
# 2.6.3 Sex Differences in Personality
twosd_test(
    n1 = 969, n2 = 716, sd1 = 3.95, sd2 = 4.47, alpha = 4.50
)

 


 

			
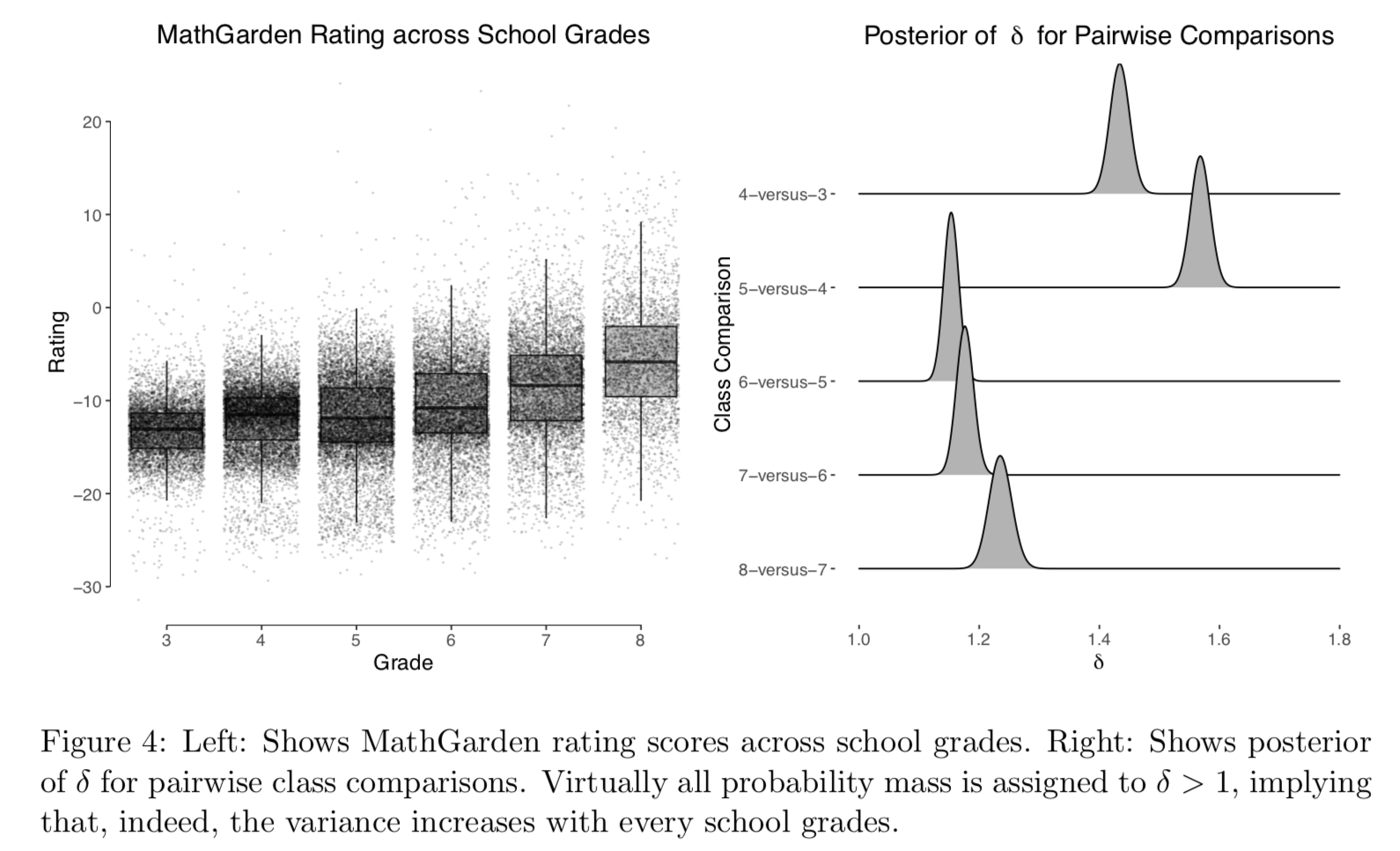
# 3.1.2 Increased Variability in Mathematical Ability
ns <- c(3280, 6007, 7549, 9160, 9395, 6410)
sds <- c(5.99, 5.39, 4.97, 4.62, 3.69, 3.08)
hyp <- c('1=2=3=4=5=6', '1,2,3,4,5,6', '1>2>3>4>5>6')

res <- ksd_test(
    hyp = hyp, ns = ns, sds = sds, alpha = 0.50
)
res$BF

# For more, run
browseVignettes(‘bfvartest’)

 

References

Böing-Messing, F. & Mulder, J. (2018). Automatic Bayes factors for testing equality and inequality-constrained hypotheses on variances. Psychometrika, 83(3), 1–32.

Borkenau, P., Hřebíčková, M., Kuppens, P., Realo, A., & Allik, J. (2013). Sex differences in variability in personality: A study in four samples. Journal of Personality, 81(1), 49-60.

Sholts, S. B., Flores, L., Walker, P. L., & Wärmländer, S. K. (2011). Comparison of coor- dinate measurement precision of different landmark types on human crania using a 3D laser scanner and a 3D digitiser: implications for applications of digital morphometrics. International Journal of Osteoarchaeology, 21(5), 535–543.

Paré, G., Cook, N. R., Ridker, P. M., & Chasman, D. I. (2010). On the use of variance per genotype as a tool to identify quantitative trait interaction effects: A report from the Women’s Genome Health Study. PLoS Genetics, 6(6), e1000981.

Kvamme, K. L., Stark, M. T., & Longacre, W. A. (1996). Alternative procedures for assessing standardization in ceramic assemblages. American Antiquity, 61(1), 116–126.

Saks, M. J., Hollinger, L. A., Wissler, R. L., Evans, D. L., & Hart, A. J. (1997). Reducing variability in civil jury awards. Law and Human Behavior, 21(3), 243–256.

Aunola, K., Leskinen, E., Lerkkanen, M.-K., & Nurmi, J.-E. (2004). Developmental Dynamics of Math Performance From Preschool to Grade 2. Journal of Educational Psychology, 96(4), 699–713.

About The Authors

Fabian Dablander

Fabian is a PhD candidate at the Psychological Methods Group of the University of Amsterdam. You can find him on Twitter @fdabl.

Don van den Bergh

Don van den Bergh is a PhD candidate at the Psychological Methods Group of the University of Amsterdam.

Alexander Ly

Alexander Ly is a postdoc at the Psychological Methods Group at the University of Amsterdam.

Eric-Jan Wagenmakers

Eric-Jan (EJ) Wagenmakers is professor at the Psychological Methods Group at the University of Amsterdam.