In an earlier blogpost I complained that the reprint of Bruno de Finetti’s masterpiece “Theory of Probability” concerns the 1970 version, and that the famous preface to the 1974 edition is missing. This blogpost provides an annotated version of this preface (de Finetti, 1974, pp. x-xiv). As the preface spans about four pages, it will take several posts to cover it all. Below, the use of italics is always as in the original text.
 
 
 
 
 
 

De Finetti’s Preface [Annotated]

“Is it possible that in just a few lines I can achieve what I failed to achieve in my many books and articles? Surely not. Nevertheless, this preface affords me the opportunity, and I shall make the attempt. It may be that misunderstandings which persist in the face of refutations dispersed or scattered over some hundreds of pages can be resolved once and for all if all the arguments are pre-emptively piled up against them.”

One senses that de Finetti was exasperated at the stubborn refusal of frequentists to see the Bayesian light. At this point in time, of course, Bayesians such as de Finetti were a species threatened with extinction. In another masterpiece with the same title (“Theory of Probability”) Harold Jeffreys also indicates his own frustration in the preface:

“Adherents of frequency definitions of probability have naturally objected to the whole system. But they carefully avoid mentioning my criticisms of frequency definitions, which any competent mathematician can see to be unanswerable. In this way they contrive to present me as an intruder into a field where everything was already satisfactory. I speak from experience in saying that students have no difficulty in following my system if they have not already spent several years in trying to convince themselves that they understand frequency theories.” (Jeffreys, 1961, p. viii)

Let’s continue with de Finetti, who proceeds to make his most iconic statement:

“My thesis, paradoxically, and a little provocatively, but nonetheless genuinely, is simply this:

PROBABILITY DOES NOT EXIST.

    The abandonment of superstitious beliefs about the existence of Phlogiston, the Cosmic Ether, Absolute Space and Time,…, or Fairies and Witches, was an essential step along the road to scientific thinking. Probability, too, if regarded as something endowed with some kind of objective existence, is no less a misleading misconception, an illusory attempt to exteriorize or materialize our true probabilistic beliefs.”

As explained in an earlier post, Augustus de Morgan expressed a similar opinion in his 1838 (!) book An Essay on Probabilities and on Their Application to Life Contingencies and Insurance Offices. And in 1874, Stanley Jevons, who was a pupil of de Morgan (see Collison Black, 1972), wrote that “Probability belongs wholly to the mind“.

De Finetti elaborates:

“This point of view is not bound up with any particular philosophical position, nor is it incompatible with any such. It is strictly reductionist in a methodological sense, in order to avoid becoming embroiled in philosophical controversy.
    Probabilistic reasoning –always to be understood as subjective– merely stems from our being uncertain about something. It makes no difference whether the uncertainty relates to an unforeseeable future, or to an unnoticed past, or to a past doubtfully reported or forgotten; it may even relate to something more or less knowable (by means of a computation, a logical deduction, etc.) but for which we are not willing or able to make the effort; and so on.
    Moreover, probabilistic reasoning is completely unrelated to general philosophical controversies, such as Determinism versus Indeterminism, Realism versus Solipsism—including the question of whether the world ‘exists’, or is simply the scenery of ‘my’ solipsistic dream. As far as Determinism and Indeterminism are concerned, we note that, in the context of gas theory or heat diffusion and transmission, whether one interprets the underlying process as being random or strictly deterministic makes no difference to one’s probabilistic opinion. A similar situation would arise if one were faced with forecasting the digits in a table of numbers; it makes no difference whether the numbers are random, or are some segment–for example, the 2001st to the 3000th digits– of the decimal expansion of π (which is not ‘random’ at all, but certain; possibly available in tables and, in principle, computable by you).
    The only relevant thing is uncertainty–the extent of our own knowledge and ignorance. The actual fact of whether or not the events considered are in some sense determined, or known by other people, and so on, is of no consequence.”

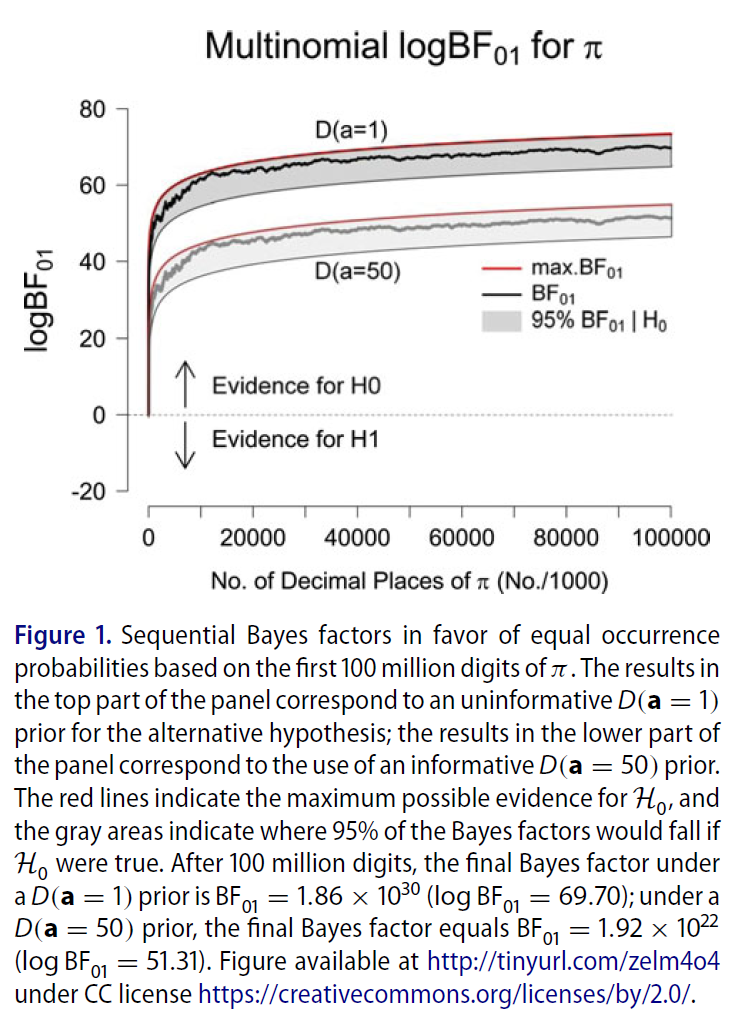
An example of this scenario is given in Gronau & Wagenmakers (2018), who computed the empirical evidence (based on the first 100 million digits) for the conjecture that the digits in the decimal expansion of π occur equally often. Below is the result of a sequential analysis under two prior distributions:

But although de Finetti condoned this use of Bayesian inference, at least in principle (and so would the mathematician George Polya, see this post), Jeffreys explicitly disagreed, or so it seems:

“This distinction shows that theoretically a probability should always be worked out completely. We have again an illustration from pure mathematics. What is the 10,000th figure in the expansion of e? Nobody knows; but that does not say that the probability that it is a 5 is 0.1. By following the rules of pure mathematics we could determine it definitely, and the statement is either entailed by the rules or contradicted; in probability language, on the data of pure mathematics it is either a certainty or an impossibility.” (Jeffreys, 1961, p. 38).

Given my own work with Quentin Gronau it should not come as a surprise that I side with de Finetti here. It is too late to ask Jeffreys, but I wonder why it is essential to condition “on the data of pure mathematics” for determining the probability that the 10,000th figure in the expansion of e is a 5, but that it would be unacceptable to condition “on the data of pure physics” for determining the outcome of a coin toss. I also wonder whether Jeffreys would accept a probability (other than 0 or 1) for a mathematical conjecture that cannot (yet) be proven. For instance, I wonder whether Jeffreys would condemn an in-between probability for the 10,000th figure in the expansion of e being a 5, but condone an in-between probability for the unproven conjecture that the digits in the expansion of e occur equally often.

More to follow…

References

Collison Black, R. D. (1972). Jevons, Bentham and De Morgan. Economica, 39, 119-134.

de Finetti, B. (1974). Theory of Probability, Vol. 1 and 2. New York: John Wiley & Sons.

de Morgan, A. (1838). An Essay on Probabilities and on Their Application to Life Contingencies and Insurance Offices. London: Longman. Freely available at https://archive.org/details/134257988

Gronau, Q. F., & Wagenmakers, E.-J. (2018). Bayesian evidence accumulation in experimental mathematics: A case study of four irrational numbers. Experimental Mathematics, 27, 277-286.

Jevons, W. S. (1877/1913). The Principles of Science: A Treatise on Logic and Scientific Method. London: MacMillan.

About The Author

Eric-Jan Wagenmakers

Eric-Jan (EJ) Wagenmakers is professor at the Psychological Methods Group at the University of Amsterdam.