The frequentist food and drug administration (FDA) has circulated a draft version of new guidelines for adaptive designs, with the explicit purpose of soliciting comments. The draft is titled “Adaptive designs for clinical trials of drugs and biologics: Guidance for industry” and you can find it here. As summarized on the FDA webpage, this draft document

 
 
 
 

“(…) addresses principles for designing, conducting and reporting the results from an adaptive clinical trial. An adaptive design is a type of clinical trial design that allows for planned modifications to one or more aspects of the design based on data collected from the study’s subjects while the trial is ongoing. The advantage of an adaptive design is the ability to use information that was not available at the start of the trial to improve efficiency. An adaptive design can provide a greater chance to detect the true effect of a product, often with a smaller sample size or in a shorter timeframe. Additionally, an adaptive design can reduce the number of patients exposed to an unnecessary risk of an ineffective investigational treatment. Patients may even be more willing to enroll in these types of trials, as they can increase the probability that subjects will be assigned to the more effective treatment.”

Bayesian Learning

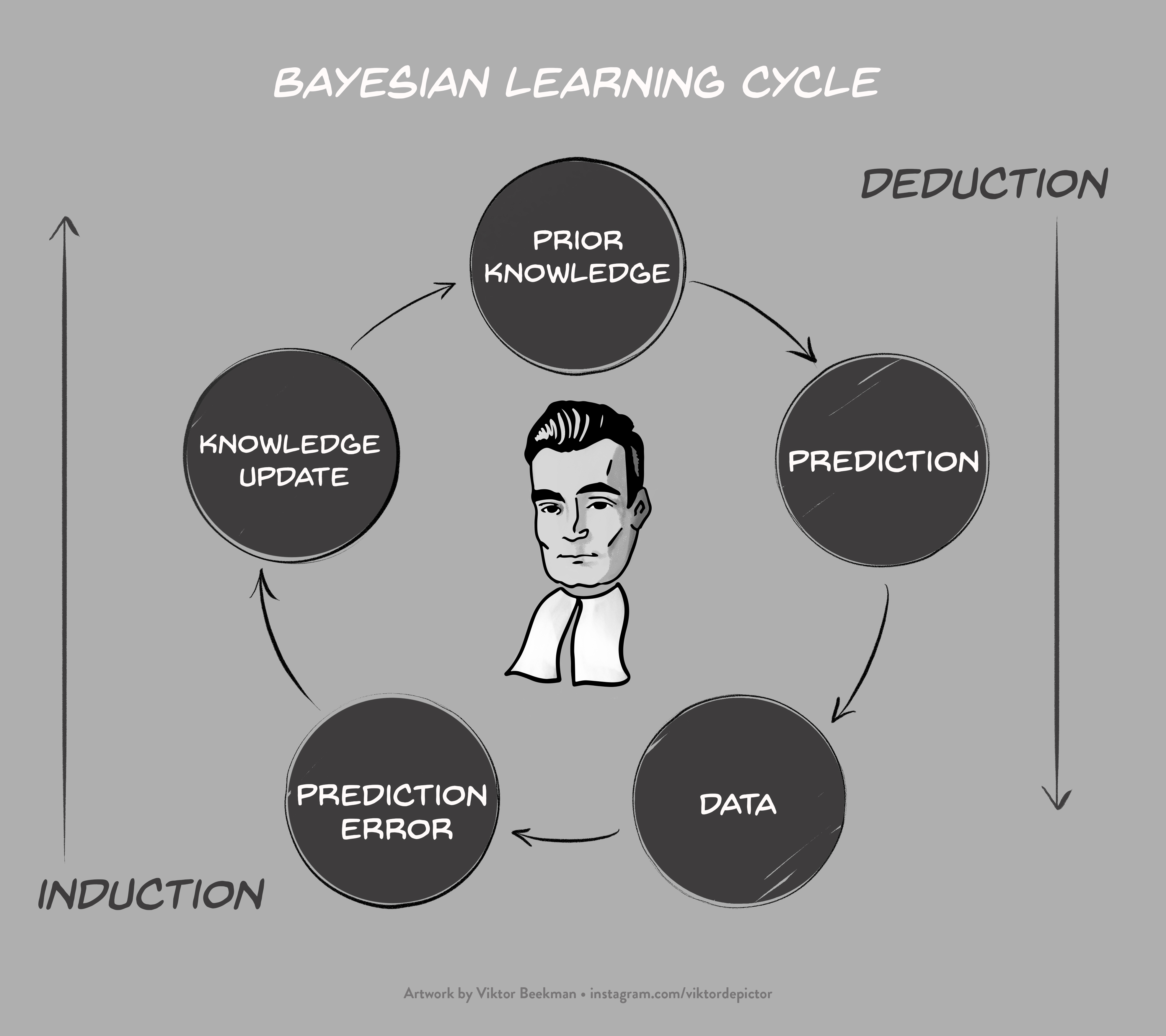
In our opinion, the FDA is spot on: sequential designs are more efficient and flexible than fixed-N designs, and should be used more often. Unfortunately, the FDA document approaches the adaptive design almost exclusively from a frequentist perspective. The use of Bayesian methods is mentioned, but it appears unlikely that any Bayesians were involved in drafting the document. This is a serious omission, particularly because the Bayesian and frequentist perspectives on sequential designs are so radically different. In short, the Bayesian formalism updates knowledge by means of relative predictive success: accounts that predicted the observed data well increase in plausibility, whereas accounts that predicted the data relatively poorly suffer a decline in plausibility. This Bayesian learning cycle, visualized in Figure 1, opens up exciting opportunities for the analysis of sequential designs.

Arguably the most prominent advantage of the Bayesian learning cycle is that –in sharp contrast to the theory of classical null-hypothesis significance testing or NHST– corrections and adjustments for adaptive designs are uncalled for, and may even result in absurdities. From the perspective of Bayesian learning, the intention with which the data were collected is irrelevant. For the interpretation of the data, it should not matter whether these data had been obtained from a fixed-N design or an adaptive design. This irrelevance is known as the Stopping Rule Principle (Berger & Wolpert, 1988).

Sequential Analysis is a Hoax

The Bayesian view on adaptive designs and sequential analysis was summarized by Anscombe (1963, p. 381):

“Sequential analysis” is a hoax… So long as all observations are fairly reported, the sequential stopping rule that may or may not have been followed is irrelevant. The experimenter should feel entirely uninhibited about continuing or discontinuing his trial, changing his mind about the stopping rule in the middle, etc., because the interpretation of the observations will be based on what was observed, and not on what might have been observed but wasn’t.”

Note that Anscombe uses the word “hoax” not in the context of sequential analysis per se, but rather in the context of the large frequentist literature that recommends a wide variety of adjustments for planning interim analyses. The term hoax refers to the idea that frequentists have managed to convince many practitioners (and apparently also institutions such as the FDA) that such adjustments are necessary. In the Bayesian framework (or that of a likelihoodist), in contrast, adjustments for the adaptive nature of a design are wholly inappropriate, and the analysis of a sequential trial proceeds in exactly the same manner as if the data had come from a fixed-N trial. Of course, in the NHST framework the sequential stopping rule is essential for the interpretation of the data, as the FDA document explains. The difference is dramatic.

[box] Recommendation 1. Acknowledge that Bayesian procedures do not require corrections for sequential analyses. Note: this does not mean that sampling plans are always irrelevant to a Bayesian. Specifically, in the *planning* stage of a trial the stopping rule does affect the expected outcomes; in the *analysis* stage, however, one conditions on the observed data, and the stopping rule is now irrelevant.
[/box] [box] Recommendation 2. Involve a Bayesian in drafting the next version. In fact, we recommend involving at least one Bayesian who advocates estimation procedures, and at least one Bayesian who advocates hypothesis testing procedures.
[/box]

After a short general introduction about Bayesian inference (without any mention of Bayesian hypothesis testing, or the notion that inferential corrections in adaptive design analysis are unwarranted), pages 20-21 of the FDA draft feature a brief discussion on “Bayesian Adaptive Designs”. We will comment on each individual fragment below:

“In general, the same principles apply to Bayesian adaptive designs as to adaptive designs without Bayesian features.”

Response: Except, of course, with respect to the absolutely crucial principle that in the Bayesian analysis of sequential designs, no corrections or adjustments whatsoever are called for — the Bayesian analysis proceeds in exactly the same manner as if the data had been collected in a fixed-N design. In contrast, in the frequentist analysis such corrections are required, regardless of whether one is interested in testing or estimation.

“One common feature of most Bayesian adaptive designs is the need to use simulations (section VI.A) to estimate trial operating characteristics.21

Footnote 21: Note that Type I error probability and power are, by definition, frequentist concepts. As such, any clinical trial whose design is governed by Type I error probability and power considerations is inherently a frequentist trial, regardless of whether Bayesian methods are used in the trial design or analysis. Nevertheless, it is common to use the term “Bayesian adaptive design,” to distinguish designs that use Bayesian methods in any way from those that do not.”

Response: Yes, in the planning stage of an experiment a Bayesian statistician may use simulations to explore the trial operating characteristics of the proposed experimental design. Before data collection has started, such simulations can be used to evaluate the expected strength of evidence for a treatment effect, or the expected precision in the estimation of the treatment effect. The results from such simulations may motivate an adjustment of the experimental design. One may even use these simulations to assess the frequentist properties of the Bayesian procedure (i.e., its performance in repeated use); for example, one may quantify how often the Bayesian outcome measure will be misleading (e.g., how often one obtains strong evidence against H0 even though H0 is true; e.g., Kerridge, 1963).

Crucially, however, in the analysis stage of an experiment, so after the data have been observed, the value and interpretation of Bayesian trial outcome measures (e.g., the Bayes factor and the posterior distribution) do not depend on the manner in which the data were collected. For example, the posterior distribution under a particular hypothesis depends only on the prior distribution, the likelihood, and the observed data; it does emphatically not depend on the intention with which the data were collected — in other words, it does not matter whether the observed data came from a fixed-N design or an adaptive design.

“Because many Bayesian methods themselves rely on extensive computations (Markov chain Monte Carlo (MCMC) and other techniques), trial simulations can be particularly resource-intensive for Bayesian adaptive designs. It will often be advisable to use conjugate priors or computationally less burdensome Bayesian estimation techniques such as variational methods rather than MCMC to overcome this limitation (Tanner 1996).”

Response: The FDA mentions variational methods and MCMC, but remains silent on the main point of contention, that is, whether adjustments for interim analyses are appropriate to begin with. Moreover, we recommend the use of prior distributions that are sensible in light of the underlying research question; only when this desideratum is fulfilled should one turn to considerations of computational efficiency. Furthermore, we recommend to preregister sensitivity analyses that present the results for a range of priors, such as those that may be adopted by hypothetical skeptics, realists, and proponents.

“Special considerations apply to Type I error probability estimation when a sponsor and FDA have agreed that a trial can explicitly borrow external information via informative prior distributions.”

Response: A Bayesian analysis does not produce a Type I error probability (i.e., a probability computed across hypothetical replications of the experiment). It produces something more desirable, namely the posterior probability of making an error for the case at hand, that is, taking into account the data that were actually observed. In the planning stage of the experiment, before the data have been observed, a Bayesian can compute the probability of finding misleading information (e.g., Schönbrodt & Wagenmakers, 2018; Stefan et al., 2018) — it is unclear whether the FDA report has this in mind or something else. In the analysis stage, again, the stopping rule ceases to be relevant as the analysis conditions only on what is known, namely the data that have been observed (e.g., Berger & Wolpert, 1988; Wagenmakers et al., 2018, pp. 40-41).

“Type I error probability simulations need to assume that the prior data were generated under the null hypothesis. This is usually not a sensible assumption, as the prior data typically being used specifically because they are not compatible with the null hypothesis. Furthermore, controlling Type I error probability at a conventional level in cases where formal borrowing is being used generally limits or completely eliminates the benefits of borrowing. It may still be useful to perform simulations in these cases, but it should be understood that estimated Type I error probabilities represent a worst-case scenario in the event that the prior data (which are typically fixed at the time of trial design) were generated under the null hypothesis.”

Response: We do not follow this fragment 100%, but it is clear that the FDA appears to labor under at least two misconceptions regarding Bayesian procedures. The first misconception is that the gold standard for Bayesian procedures is to control the Type I error rate. As mentioned above, what the FDA is missing here is that Bayesian procedures produce something different, something more desirable, and something more relevant, namely the probability of making an error for the actual case at hand. If the posterior probability that a treatment is beneficial is .98, this means that, given the observed data and the prior, there is a .02 probability that the claim “this treatment is beneficial” is in error. This is a much more direct conclusion then can ever be obtained by “controlling the probability that imaginary data sets show a more extreme result, given that the null hypothesis is true” (i.e., computing a p-value and comparing it to a fixed value such as .05) As Bayesian pioneer Harold Jeffreys famously stated:

“What the use of P implies, therefore, is that a hypothesis that may be true may be rejected because it has not predicted observable results that have not occurred. This seems a remarkable procedure” (Jeffreys, 1961, p. 385).

[box] Recommendation 3. Acknowledge that control of Type I error rate is not the holy grail of every statistical method. A more desirable goal is arguably to assess the probability of making a mistake, for the case at hand.
[/box]

The second misconception is that Bayesian procedures differ from frequentist procedures mainly because Bayesian procedures can include additional information. Yet this is only one advantage. Bayesian inference also differs from frequentist inference because the former allows one to learn, allows probabilities to be attached to parameters and hypotheses, demands that one conditions on what is known (i.e., the observed data) and averages across what is unknown; Bayesian inference generally respects the Stopping Rule Principle and the Likelihood Principle (which allows a simple implementation of sequential testing without the need for corrections), and it allows researchers to quantify evidence, both in favor of the alternative hypothesis and in favor of the null hypothesis (in case one wishes to engage in hypothesis testing). Below is a table of desiderata fulfilled by Bayesian inference and not fulfilled by frequentist inference, as taken from Wagenmakers et al. (2018):

The FDA draft document concludes:

“A comprehensive discussion of Bayesian approaches is beyond the scope of this document. As with any complex adaptive design proposal, early discussion with the appropriate FDA review division is recommended for adaptive designs that formally borrow information from external sources.”

Response: We agree that in the planning stage, it is important to take the sequential nature of the design into consideration. In the analysis stage, however, the Bayesian approach is almost embarrassingly simple: the data may be analyzed just as if they came from a fixed-N design. The intention to stop or continue the trial had the data turned out differently than they did is simply not relevant for drawing conclusions from data.

Conclusion and Recommendations

The FDA is correct to call more attention to adaptive design and sequential analysis of clinical trial data, as such methods greatly increase the efficiency of the testing procedure. One may even argue that a non-sequential procedure is ethically questionable, as it stands a good chance of wasting valuable resources from both doctors and patients.

Unfortunately, however, the current FDA draft presents an incomplete and distorted picture of Bayesian inference and what it has to offer for adaptive designs. To remedy this situation, we issue the following five recommendation for the FDA as they seek to improve their manuscript:

1. Acknowledge that Bayesian procedures do not require corrections for sequential analyses.
2. Involve a team of Bayesians in drafting the next version. Include at least one Bayesian who advocates estimation procedures, and at least one Bayesian who advocates hypothesis testing procedures.
3. Acknowledge that control of Type I error rate is not the holy grail of every statistical method. A more desirable goal is arguably to assess the probability of making a mistake, for the case at hand.
4. When Bayesian approaches are discussed, make a clear distinction between planning (before data collection, when the stopping rule is relevant) and inference (after data collection, when the stopping rule is irrelevant).
5. Bayesian guidelines for adaptive designs are fundamentally different from frequentist guidelines. Ideally, the FDA recommendations are written to respect this difference, and would feature separate “Guidelines for frequentists” and “Guidelines for Bayesians”.

References

Anscombe, F. J. (1963). Sequential medical trials. Journal of the American Statistical Association, 58, 365-383.

Berger, J. O., & Wolpert, R. L. (1988). The Likelihood Principle (2nd ed.). Hayward, CA: Institute of Mathematical Statistics.

Jeffreys, H. (1961). Theory of Probability (3rd ed). Oxford: Oxford University Press.

Jevons, W. S. (1874/1913). The Principles of Science: A Treatise on Logic and Scientific Method. London: MacMillan.

Kerridge, D. (1963). Bounds for the frequency of misleading Bayes inferences. The Annals of Mathematical Statistics, 34, 1109-1110.

Schönbrodt, F. D., & Wagenmakers, E.-J. (2018). Bayes factor design analysis: Planning for compelling evidence. Psychonomic Bulletin & Review, 25, 128-142. Open access.

Stefan, A. M., Gronau, Q. F., Schönbrodt, F. D., & Wagenmakers, E.-J. (2018). A tutorial on Bayes factor design analysis with informed priors. Manuscript submitted for publication.

U.S. Department of Health and Human Services (2018). Adaptive designs for clinical trials of drugs and biologics: Guidance for industry. Draft version, for comment purposes only.

Wagenmakers, E.-J., Marsman, M., Jamil, T., Ly, A., Verhagen, A. J., Love, J., Selker, R., Gronau, Q. F., Šmíra, M., Epskamp, S., Matzke, D., Rouder, J. N., Morey, R. D. (2018). Bayesian inference for psychology. Part I: Theoretical advantages and practical ramifications. Psychonomic Bulletin & Review, 25, 35-57. Open access.

About The Authors

Eric-Jan Wagenmakers

Eric-Jan (EJ) Wagenmakers is professor at the Psychological Methods Group at the University of Amsterdam.

Quentin F. Gronau

Quentin is a PhD candidate at the Psychological Methods Group of the University of Amsterdam.

Angelika Stefan

Angelika is a PhD candidate at the Psychological Methods Group of the University of Amsterdam.

Gilles Dutilh

Gilles is a statistician at the Clinical Trial Unit of the University Hospital in Basel, Switzerland. He is responsible for statistical analyses and methodological advice for clinical research.

Felix Schönbrodt

Felix Schönbrodt is Principal Investigator at the Department of Quantitative Methods at Ludwig-Maximilians-Universität (LMU) Munich.