WARNING: This post is about chess. If you don’t play chess you might want to skip this post.
During a week-long family vacation I engaged obsessively in both the highest and the lowest form of human intellectual activity. Obviously the highest form is chess endgame study composition; the lowest form surely is online “bullet” chess. Miraculously, my bullet chess adventures ended up inspiring the endgame compositions. But in order not to give away the solutions, I will discuss the bullet inspiration later. The problems that I “composed” are meant to entertain; they are not meant as serious compositions with depth and subtlety. Since the positions are also highly unusual, I am inclined to classify them as “grotesque” problems (the GOAT of the genre being the brilliant Ottó Bláthy). But Bláthy’s problems are much stranger still, so perhaps the problems below are only semi-grotesque, or grotesque-esque. [Disclaimer: I have not carefully checked whether my problems are original. If you know of any conceptually related predecessors, please let me know and I will adjust this post to give the appropriate credit.] Let’s go:
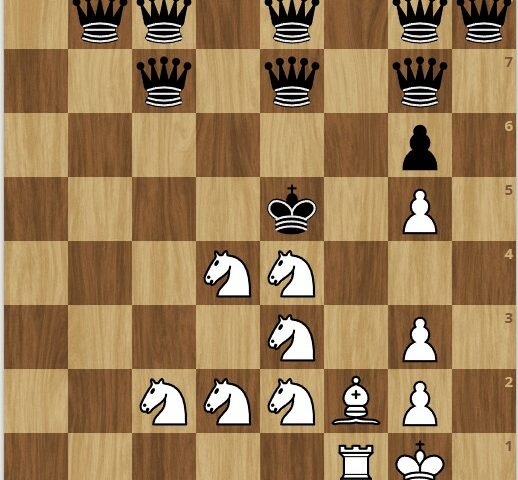
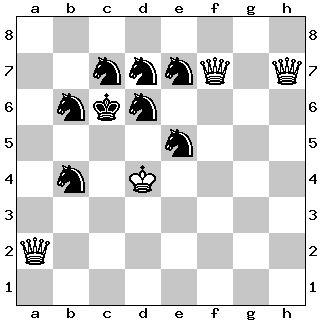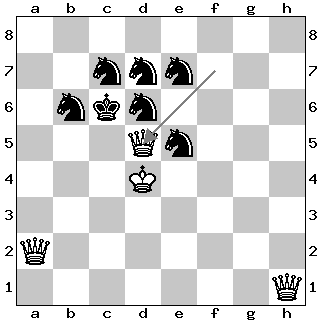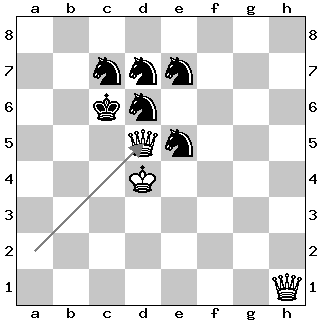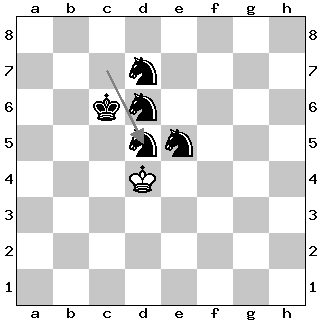
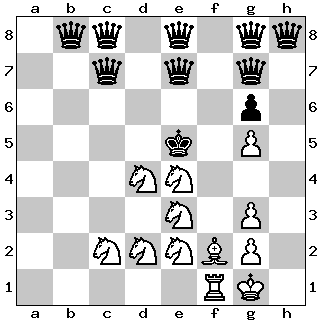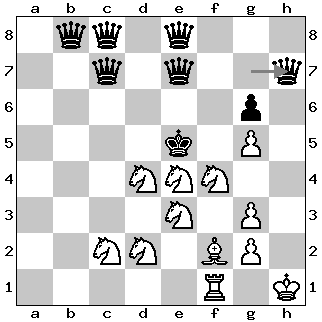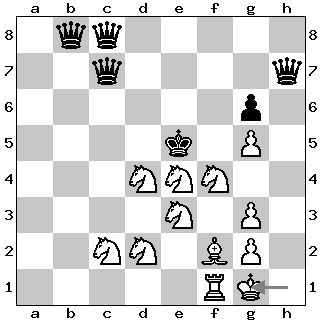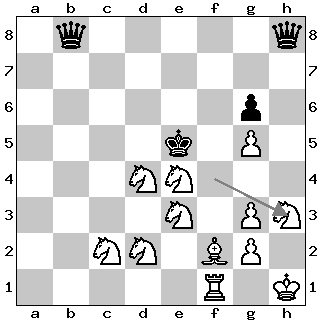
Problem 1: Three Queens vs. Seven Knights
In the diagram below, three white queens are up against no less than seven black knights. Moreover, two of the queens are under attack. Swift action is needed to avoid defeat. Hence the assignment: White to play and draw. The solution is given at the end of this post.
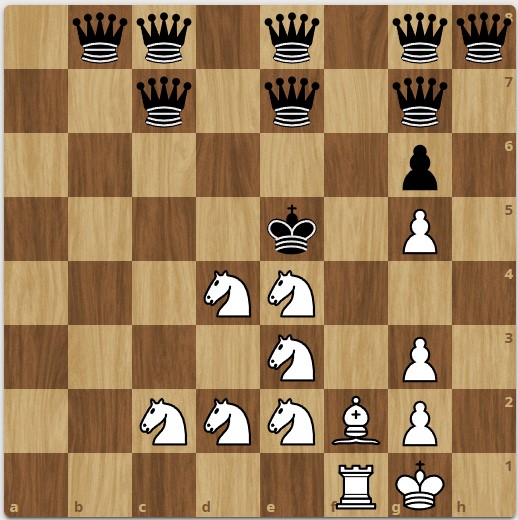
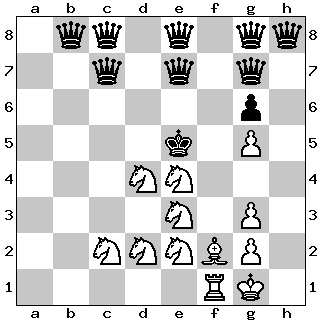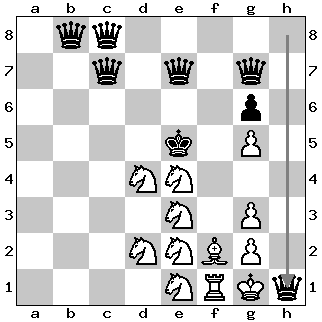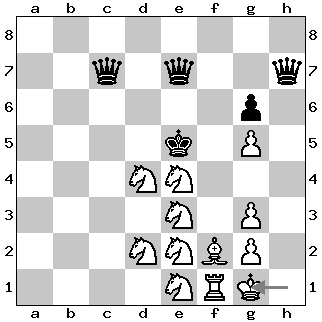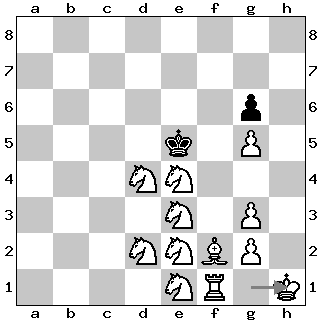
Problem 2: Six Knights vs. Eight Queens
The position below is balancing on a knife’s edge: six knights, one rook, and one bishop are usually no match for eight(!) queens; however, the black king is periliously placed. Only one move by white wins; another moves draws; all other moves lose. The assignment is therefore: White to play and win. The solution is given at the end of this post.
Bullet Chess Inspiration
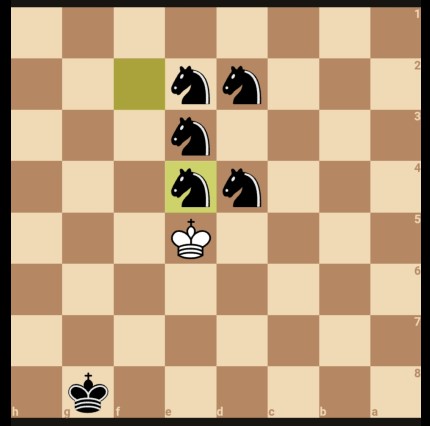
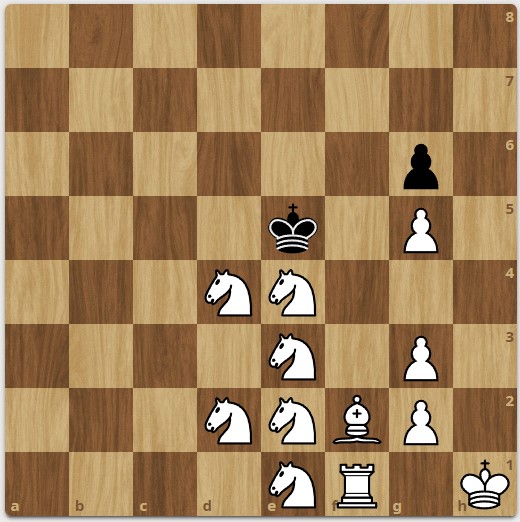
Most chess enthusiasts will have noticed that the two problems feature an abundance of knights. The cause of this was an innocent bullet game in which I had the black pieces. In this game, my opponent was dead-lost, low on time, but stubbornly refused to resign. As dictated by custom, I wanted to tease my opponent, rub salt in their wounds, teach them a lesson, and generally keep life interesting by underpromoting all my remaining pawns to knights. After successfully completing this task, I set out to swarm the white king with my knights and deliver a rightly deserved and highly emberassing checkmate. I made a random move bringing one of my knights closer to the white king… and then BOOM:
Stalemate! After recovering from the shock, I felt that the stalemate was actually esthetically pleasing — all the knights fulfill a role and stalemate the white king in the center of the board. This experience motivated the problems above.
Solution to Problem 1
All three queens need to be sacrificed to produce stalemate: 1. Qh1!+ Nd5 and the three queens are successively exchanged/sacrificed on the d5 square; the capture of the third queen creates a surprise stalemate in the middle of the board:
A moving gif of the solution:
Solution to Problem 2
The solution that draws is 1. Ne1? This move looks immediately decisive, as the e1-knight eyes two mating squares: d3 and f3. However, black can escape by sacrificing all of their eight queens on the h1/h2 squares, with stalemate as a result:
The only winning move is 1. Nf4! This move also comes with a dual mating threat — 2. Nf4-d3 and the surprising 2. Nd4-f3. The difference with 1. Ne1? is that the knight on f4 can interrupt the lemming-like sequence of queen sacrifices by interpolating on the h3 square at the appropriate moment. For instance:
About The Author

Eric-Jan Wagenmakers
Eric-Jan (EJ) Wagenmakers is professor at the Psychological Methods Group at the University of Amsterdam.