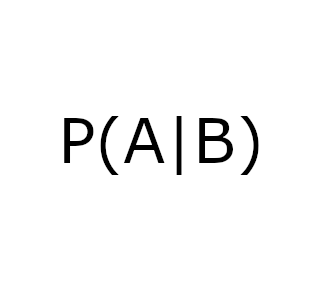The universal notation for “the probability of A given B” is p(A | B). We were surprised to learn that the vertical stroke was first introduced by none other than… Sir Harold Jeffreys! At least Jeffreys himself seems to think so, and the sentiment is echoed on the website “Earliest Uses of Symbols in Probability and Statistics” Specifically, on page 15 of his brilliant book “Scientific Inference” (1931), Jeffreys introduces the vertical stroke notation:

And on page 25 of the even more brilliant book “Theory of Probability” (1939), Jeffreys explains the history of the notation in more detail:

So the man who invented the Bayesian hypothesis test (together with Dorothy Wrinch; but see Etz & Wagenmakers, 2017), the man who inferred that the earth’s core was not solid, and the man who first proposed the vertical stroke notation for conditional probability are one and the same. For more background on Harold Jeffreys’s contributions to probability theory we recommend the riveting book by Howie (2002).

Someone Badly Needs to Fix the Wikipedia Entry for Harold Jeffreys

As an aside, the Wikipedia entry on Jeffreys hardly does justice to his groundbreaking contributions in astronomy, geophysics, and statistics. The second sentence of the Wiki entry (accessed Jan 28, 2019) goes “The book that he and Bertha Swirles wrote Theory of Probability, which first appeared in 1939, played an important role in the revival of the Bayesian view of probability.” — this is incorrect: Sir Jeffreys and Lady Jeffreys co-authored the 1946 book Methods of Mathematical Physics, but not Theory of Probability.

The Wiki entry, which is embarrassingly short, later mentions: “The textbook Probability Theory: The Logic of Science, written by the physicist and probability theorist Edwin T. Jaynes, is dedicated to Jeffreys. The dedication reads, “Dedicated to the memory of Sir Harold Jeffreys, who saw the truth and preserved it.” A nice tidbit, no doubt, but does it really warrant mention in a one-page entry on one of the most impressive scientists of the past century? Moreover, a substantial portion of the entry is spent bemoaning Jeffreys’s reluctance to accept the continental drift hypothesis (e.g., Jeffreys, 1976, pp. 481-492), which again is not representative of the many contributions throughout his career.

One last example. The Wiki entry states: “It is only through an appendix to the third edition of Jeffreys’ book Scientific Inference that we know about Mary Cartwright’s method of proving that the number π is irrational.” Again, a nice tidbit, but surely not worth more than a bare mention even in an exhaustive biography. If tidbits need to be included at all, we respectfully suggest to mention the fact that Jeffreys introduced the symbol for conditional probability.

References

Etz, A. & Wagenmakers, E.-J. (2017). J. B. S. Haldane’s contribution to the Bayes factor hypothesis test. Statistical Science, 32, 313-329.Open Access

Howie, D. (2002). Interpreting probability: Controversies and developments in the early twentieth century. Cambridge: Cambridge University Press.

Jeffreys, H. (1931). Scientific Inference. Cambridge: Cambridge University Press.

Jeffreys, H. (1939). Theory of Probability. Oxford: Oxford University Press.

Jeffreys, H. (1976). The Earth: Its Origin, History and Physical Constitution. Cambridge: Cambridge University Press.

About The Authors

Eric-Jan Wagenmakers

Eric-Jan (EJ) Wagenmakers is professor at the Psychological Methods Group at the University of Amsterdam.

Maarten Marsman

Maarten Marsman is assistent professor at the Psychological Methods Group at the University of Amsterdam.