Andrew Gelman and Christian Robert are two of the most opinionated and influential statisticians in the world today. Fear and anguish strike into the heart of the luckless researchers who find the fruits of their labor discussed on the pages of the duo’s blogs: how many fatal mistakes will be uncovered, how many flawed arguments will be exposed? Personally, we celebrate every time our work is put through the Gelman-grinder or meets the Robert-razor and, after a thorough evisceration, receives the label “not completely wrong”, or –thank the heavens– “Meh”. Whenever this occurs, friends send us enthusiastic Emails along the lines of “Did you see that? Your work is discussed on the Gelman/Robert blog and he did not hate it!” (true story).
It is therefore with considerable trepidation (a fancy word for fear and anguish) that we are going to discuss the agreements and disagreements with respect to a manuscript that Gelman and Robert recently co-authored, titled “Abandon Statistical Significance”. This manuscript is a response to the paper “Redefine Statistical Significance” that we have discussed here in the last eight posts. The entire team (henceforth: the Abandoners) consists of Blakeley McShane, David Gal, Andrew Gelman, Christian Robert, and Jennifer Tackett.
First and foremost, it is clear that the Abandoners and the Redefiners agree on many points. Here is a non-exhaustive list (note that we do not speak for all of the Redefiners; we present our personal opinion):
Like 1. As the group name suggests, the Abandoners recommend “abandoning the null hypothesis significance testing paradigm entirely”. In principle, we agree. Pure pragmatism was what motivated the Redefiners to call for a lower threshold (instead of abandoning thresholds altogether). We do not believe that null hypothesis significance testing will go away any time soon, so we compromised and tried to protect researchers from the p-value procedure’s most flagrant excesses.
Like 2. We agree with the Abandoners that the .005 level alone is insufficient to overcome difficulties with replication (or statistical abuse in general).
Like 3. We agree that statistical analysis is frustrated by issues such as noisy measurement, “the garden of forking paths”, motivated reasoning, hindsight bias, and many others.
Like 4. We agree that arbitrary thresholds (of whatever kind) can promote statistical abuse.
Like 5. We agree that, once sample size is increased to have a better chance of meeting the more stringent .005 threshold, this may then again result in overconfidence.
There are, however, points of disagreement. Below we list three:
Disagreement 1. For authors, the Abandoners recommend
“(…) studying and reporting the totality of their data and relevant results (…) For example, they might include in their manuscripts a section that directly addresses each in turn in the context of the totality of their data and results. For example, this section could discuss the study design in the context of subject-matter knowledge and expectations of effect sizes, for example as discussed by Gelman and Carlin [2014]. As another example, this section could discuss the plausibility of the mechanism by (i) formalizing the hypothesized mechanism for the effect in question and explicating the various components of it, (ii) clarifying which components were measured and analyzed in the study, and (iii) discussing aspects of the data results that support the proposed mechanism as well as those (in the full data) that are in conflict with it.”
This general advice is eminently sensible, but it is not sufficiently explicit to replace anything. Rightly or wrongly, the p-value offers a concrete and unambiguous guideline for making key claims; the Abandoners wish to replace it with something that can be summarized as “transparency and common sense”. Of course we all like transparency and common sense (as long as it is our common sense, and not that of our academic adversary), but “discussing aspects of the data that support the proposed mechanism” is too vague — what exactly should be “discussed”, and how? When should a skeptic be convinced that the authors aren’t fooling themselves and are just presenting noise? How exactly should the statistical analysis support the claims of interest? Perhaps the Abandoners are right, and proper judgement requires a combination of highly context-dependent ingredients that are then tossed in a subjective blender of statistical acumen. This is fine, but pragmatically, the large majority of researchers won’t use the sophisticated statistical blender — they won’t know how it works, the manual is missing, and consequently they will stick to what they know, which is the p-value meat cleaver.
Disagreement 2. The Abandoners’ critique the UMPBTs –the uniformly most powerful Bayesian tests– that features in the original paper. This is their right (see also the discussion of the 2013 Valen Johnson PNAS paper), but they ignore the fact that the original paper presented a series of other procedures that all point to the same conclusion: p-just-below-.05 results are evidentially weak. For instance, a cartoon on the JASP blog explains the Vovk-Sellke bound. A similar result is obtained using the upper bounds discussed in Berger & Sellke (1987) and Edwards, Lindman, & Savage (1963). We suspect that the Abandoners’ dislike of Bayes factors (and perhaps their upper bounds) is driven by a disdain for the point-null hypothesis. That is understandable, but the two critiques should not be mixed up. The first question is Given that we wish to test a point-null hypothesis, do the Bayes factor upper bounds demonstrate that the evidence is weak for p-just-below-.05 results? We believe they do, and in this series of blog posts we have provided concrete demonstrations.
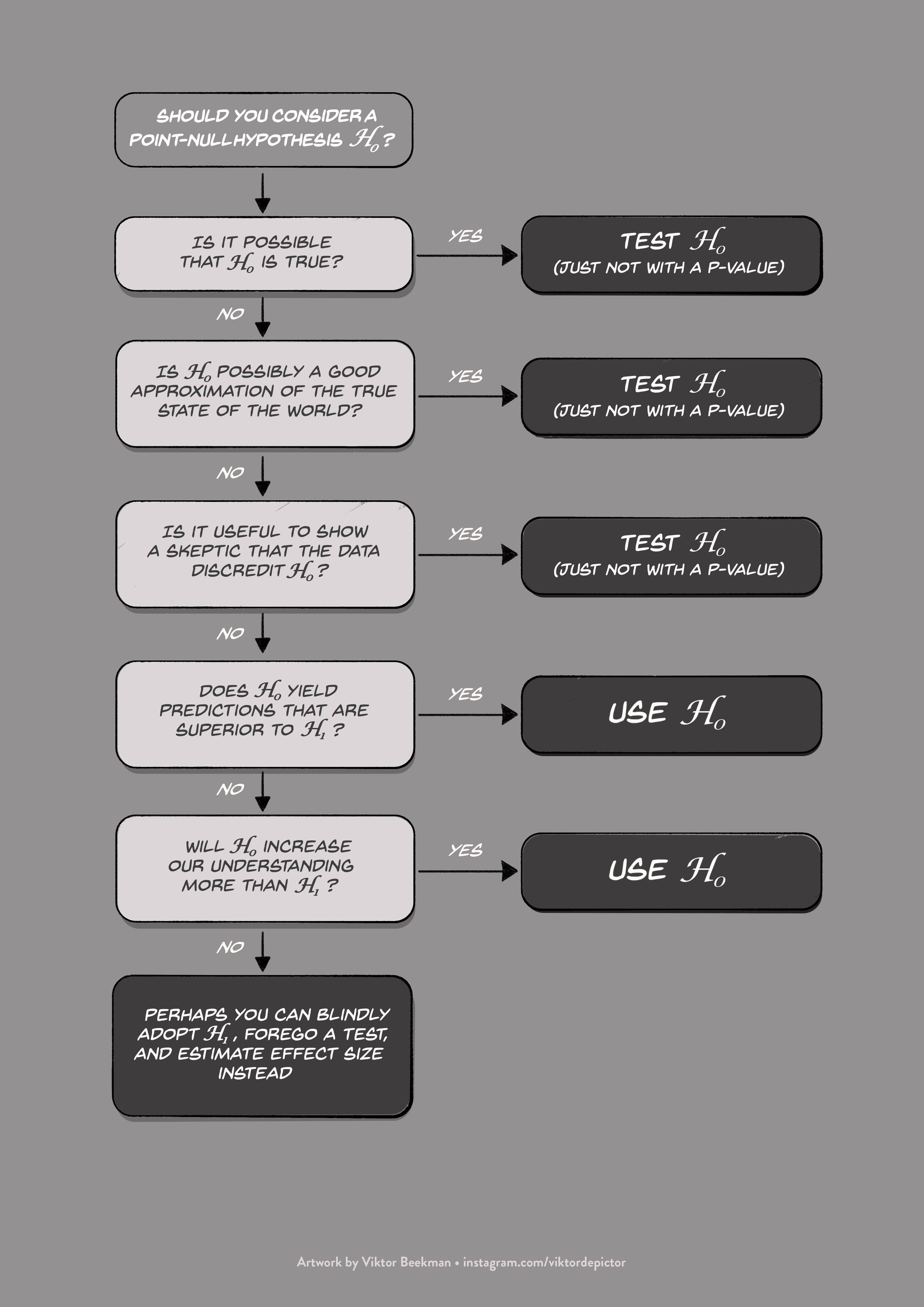
Disagreement 3. One of the Abandoners’ favorite arguments is that the point-null hypothesis is usually neither true nor interesting. So why test it? This echoes the opinion of researchers like Meehl and Cohen. We believe, however, that Meehl and Cohen were overstating their case. Inspired by the statistical philosophy of Harold Jeffreys, and assisted by our experience in experimental psychology, we have created a flowchart to illustrate when the point-null hypothesis can come into consideration:
Figure 1. A flowchart to clarify the scenarios for which the point-null hypothesis is useful.
In this post, we will discuss the first two choices from the flow chart. The other choices will be discussed in a next post.
Choice 1: Is the point-null hypothesis ever exactly true?
We borrow a generic example from Cornfield (1966): is whisky an effective cure against snake bite? To us, the point-null seems reasonable: if the whisky does not act on the relevant biological process, the treatment will be ineffective. But the example can easily be made more extreme. For instance, consider the claim that the healing powers of whisky only manifest themselves for single malts. In other words, the placebo condition involves blends. It is hard to see what kind of argument could be made for a difference, however miniscule, between the curative impact of single malts versus blends. This example can be made more and more ridiculous (e.g., the curative impact is only present for bites by Arizona Mountain Kingsnakes that occur on days of the full moon).
Choice 2: Is the point-null hypothesis just a mathematically convenient approach?
This defense against the charge that the point-null is always false was mentioned by Harold Jeffreys (of course), but several other statisticians brought it up as well. Here is what Cornfield had to say:
“There is a psychological difficulty felt by some to the concentration of a lump of probability at a single point. Thus, even though entirely convinced of the ineffectiveness of whiskey in the treatment of snake bite they would hesitate to offer prior odds of p to 1-p that the true mortality difference between treated and untreated is zero to an arbitrarily large number of decimal places.[EJ&QG: Note that “p” here refers to the prior probability for the null hypothesis, not to the classical p-value] But if the concentration is regarded as the result of a limiting process it appears unexceptional. To say that the treatment is ineffective means that the hypothesis Hδ: |θ| ≤ |δ| is true, where δ is quite small, perhaps of the order of 1 death among all persons bitten by venomous snakes in a decade, but not specifiable more precisely. For finite sized samples the probability of rejecting either H0 or Hδ will be nearly equal, and concern about the high probability of rejecting one is equivalent to concern about rejecting the other.” (Cornfield, 1966, p. 582)
To make this even more concrete, we will introduce three kangaroos (finally!). The first kangaroo was introduced in a blog post by Andrew Gelman when he described the following situation:
“when effect size is tiny and measurement error is huge, you’re essentially trying to use a bathroom scale to weigh a feather—and the feather is resting loosely in the pouch of a kangaroo that is vigorously jumping up and down.” (Andrew Gelman, blog post, April 21, 2015)
This scenario is captured in Figure 1. This “Gelman kangaroo” perfectly captures the argument of those who dislike the point-null hypothesis; there is always an effect (the feather in the pouch) but measurement error may make it nearly impossible to detect.
Figure 2. The Gelman kangaroo. There is an effect (the feather in the pouch) but measurement error may make it nearly impossible to detect.
However, consider Figure 3 and behold two Gelman kangaroos. The Gelman kangaroo in the left panel is the same as before: it has a feather in its pouch, and strictly speaking the null hypothesis is false. The Gelman kangaroo in the right panel, however, has an empty pouch, and the null hypothesis is exactly true.
Figure 3. Two Gelman kangaroos. The left kangaroo has a feather in its pouch, symbolizing the presence of an effect; the right kangaroo lacks a feather, symbolizing the absence of an effect. For an assessment of the situation, it is irrelevant whether we believe which kangaroo best represents the state of the world.
The point of the figure is exactly that mentioned by Cornfield: if the true effect is as big as the feather in the pouch of a kangaroo that’s vigorously jumping up and down, it does not matter at all whether we assume that the true effect is exactly zero or whether it is very close to zero. The result of our statistical tests will be virtually unaffected.
Take-Home Message
When someone claims the null-hypothesis is never true, just send them a Gelman kangaroo or two.
Like this post?
Subscribe to the JASP newsletter to receive regular updates about JASP including the latest Bayesian Spectacles blog posts! You can unsubscribe at any time.
References
Berger, J. O., & Sellke, T. (1987). Testing a point null hypothesis: The irreconcilability of p values and evidence. Journal of the American Statistical Association, 82, 112-139.
Cornfield, J. (1966). A Bayesian test of some classical hypotheses—with applications to sequential clinical trials. Journal of the American Statistical Association, 61, 577-594.
Edwards, W., Lindman, H., & Savage, L. J. (1963). Bayesian statistical inference for psychological research. Psychological Review, 70, 193-242.
Johnson, V. E. (2013). Revised standards for statistical evidence. Proceedings of the National Academy of Sciences of the United States of America, 110, 19313-19317.
McShane. B. B., Gal, D., Gelman, A., Robert, C., & Tackett, J. L. (2017). Abandon statistical significance. Preprint.
About The Authors

Eric-Jan Wagenmakers
Eric-Jan (EJ) Wagenmakers is professor at the Psychological Methods Group at the University of Amsterdam.

Quentin Gronau
Quentin is a PhD candidate at the Psychological Methods Group of the University of Amsterdam.