This post is a teaser for Maier, Bartoš, & Wagenmakers (2020). Robust Bayesian meta-analysis: Addressing publication bias with model-averaging. Preprint available on PsyArXiv: https://psyarxiv.com/u4cns
Abstract
“Meta-analysis is an important quantitative tool for cumulative science, but its application is frustrated by publication bias. In order to test and adjust for publication bias, we extend model-averaged Bayesian meta-analysis with selection models. The resulting Robust Bayesian Meta-analysis (RoBMA) methodology does not require all-or-none decisions about the presence of publication bias, is able to quantify evidence in favor of the absence of publication bias, and performs well under high heterogeneity. By model-averaging over a set of 12 models, RoBMA is relatively robust to model misspecification, and simulations show that it outperforms existing methods. We demonstrate that RoBMA finds evidence for the absence of publication bias in Registered Replication Reports and reliably avoids false positives. We provide an implementation in R and JASP so that researchers can easily apply the new methodology to their own data.”
Component 1: Model-Averaged Bayesian Meta-Analysis
Component 2: Selection Models
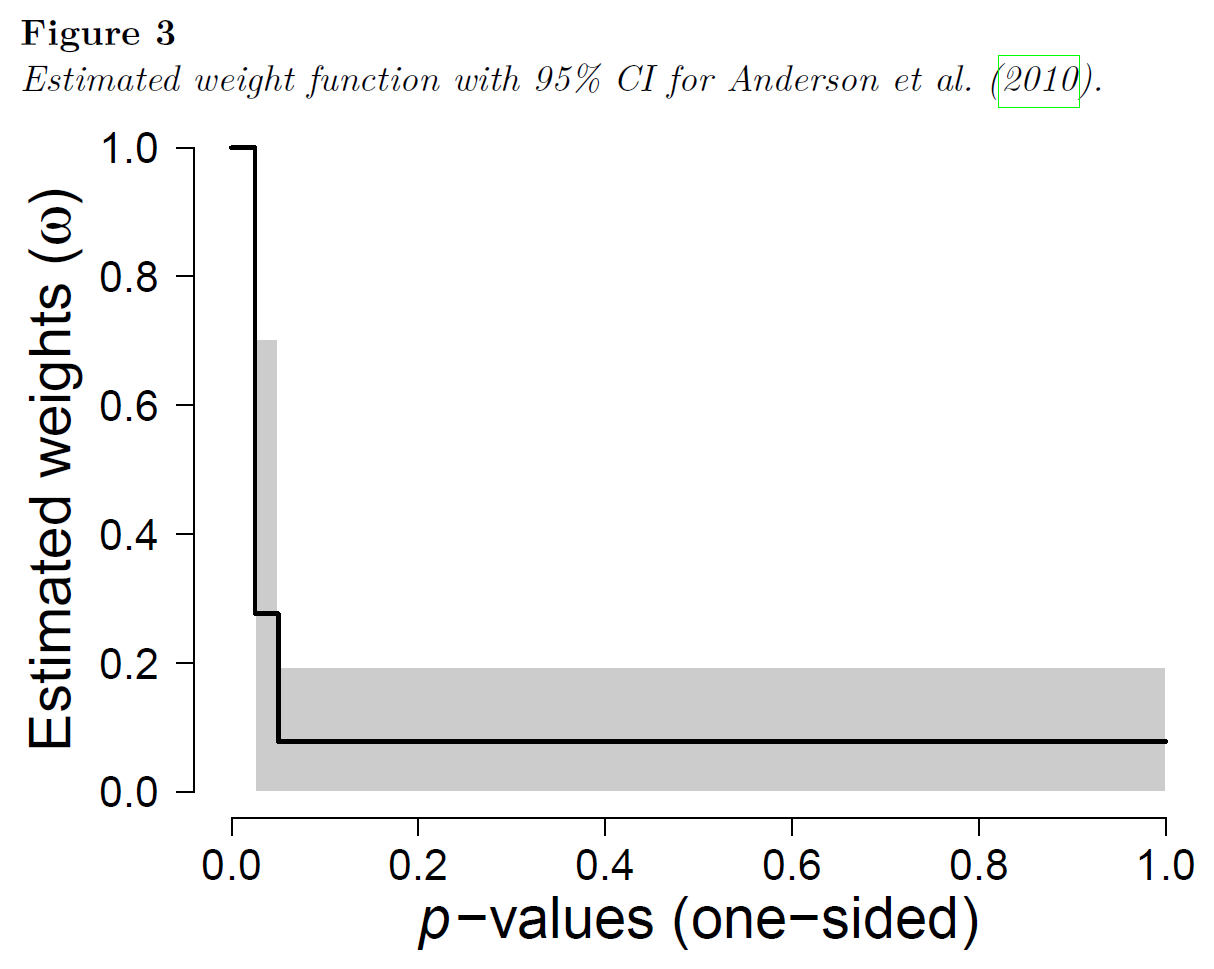
“Selection models use weighted distributions to account for the proportion of studies that are missing because they yielded non-significant results. The researcher specifies the p-value cut-offs that drive publication bias (usually p = .05). The selection model then estimates how likely studies in nonsignificant intervals are to be published compared to the interval with the highest publication probability (usually p < .05). The pooled effect size estimate accounts for the estimated publication bias by giving more weight to studies in intervals with lower publication probability (usually non-significant studies).”
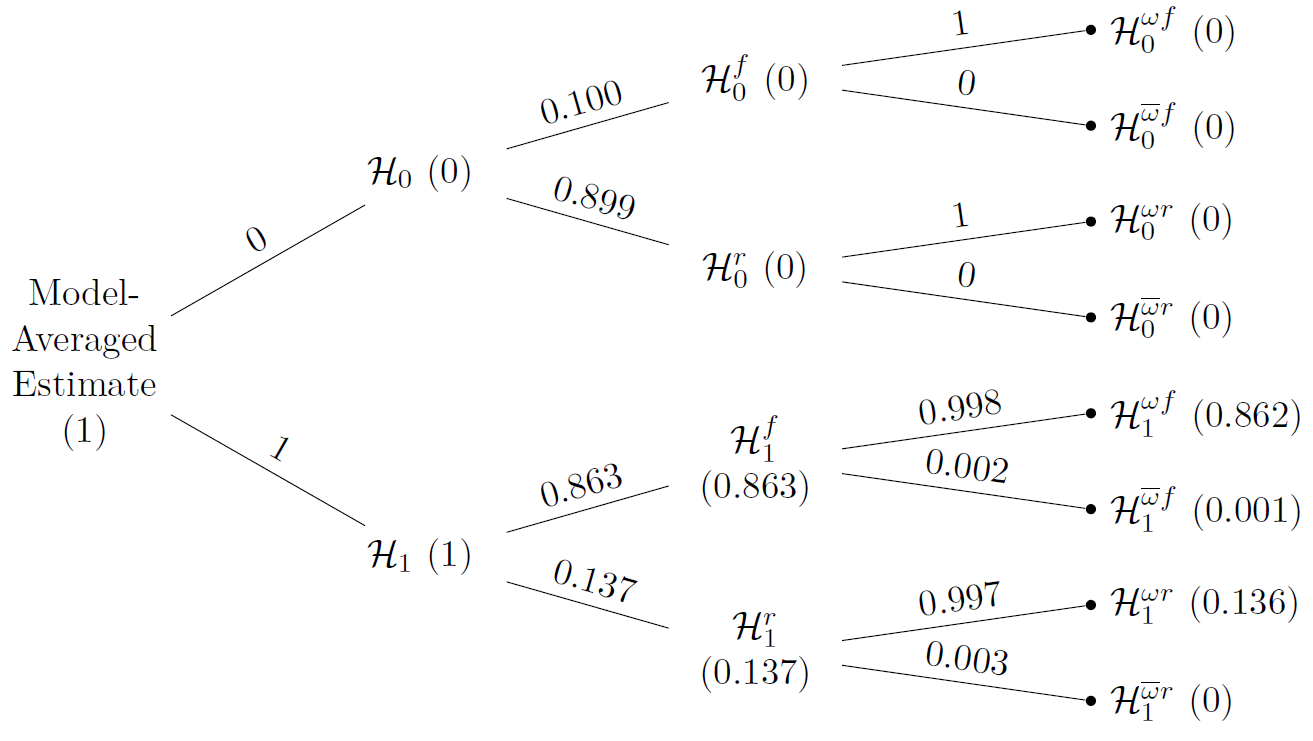
Combining Model-Averaged Bayesian Meta-Analysis and Selection Models: Robust Bayesian Meta-Analysis (RoBMA)
“We propose Robust Bayesian Meta-Analysis (RoBMA), a Bayesian multi-model method that aims to overcome the limitations of existing procedures. RoBMA is an extension of BMA obtained by adding selection models to account for publication bias. This allows model-averaging across a larger set of models, ones that assume publication bias and
ones that do not.”
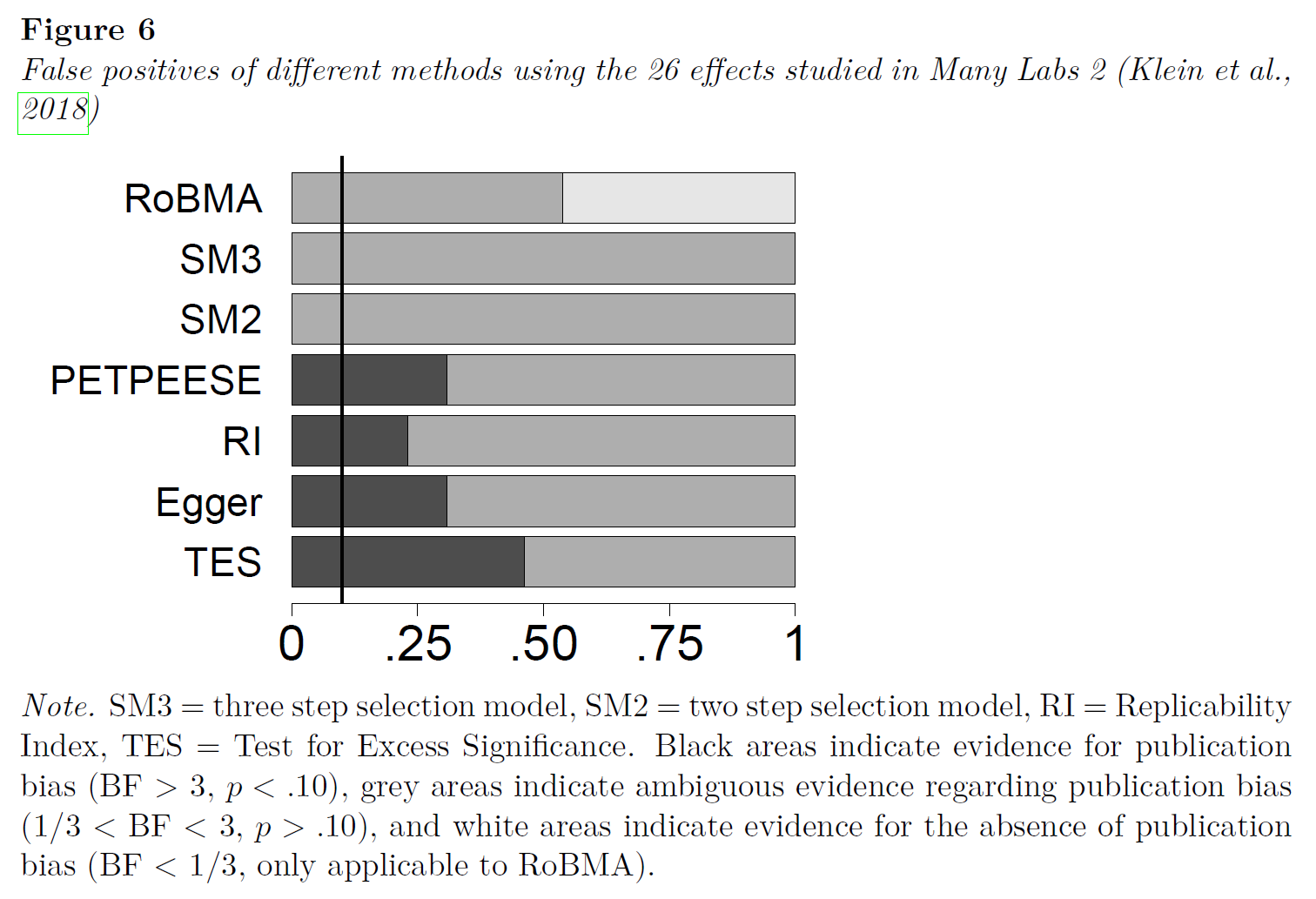
Testing False Positives on Many Labs 2
“It is hard to assess the performance of different methods on published meta-analyses since the true parameters are usually unknown. However, it is possible to assess the false positive rate of tests for publication bias using Registered Replication Reports (Chambers, 2013, 2019). Here we know that all primary studies are published regardless of the result; therefore, if a method detects publication bias, this is a false positive finding. In addition, Registered Replication Reports allow an empirical test of RoBMA’s ability to quantify evidence in favor of the absence of publication bias.”
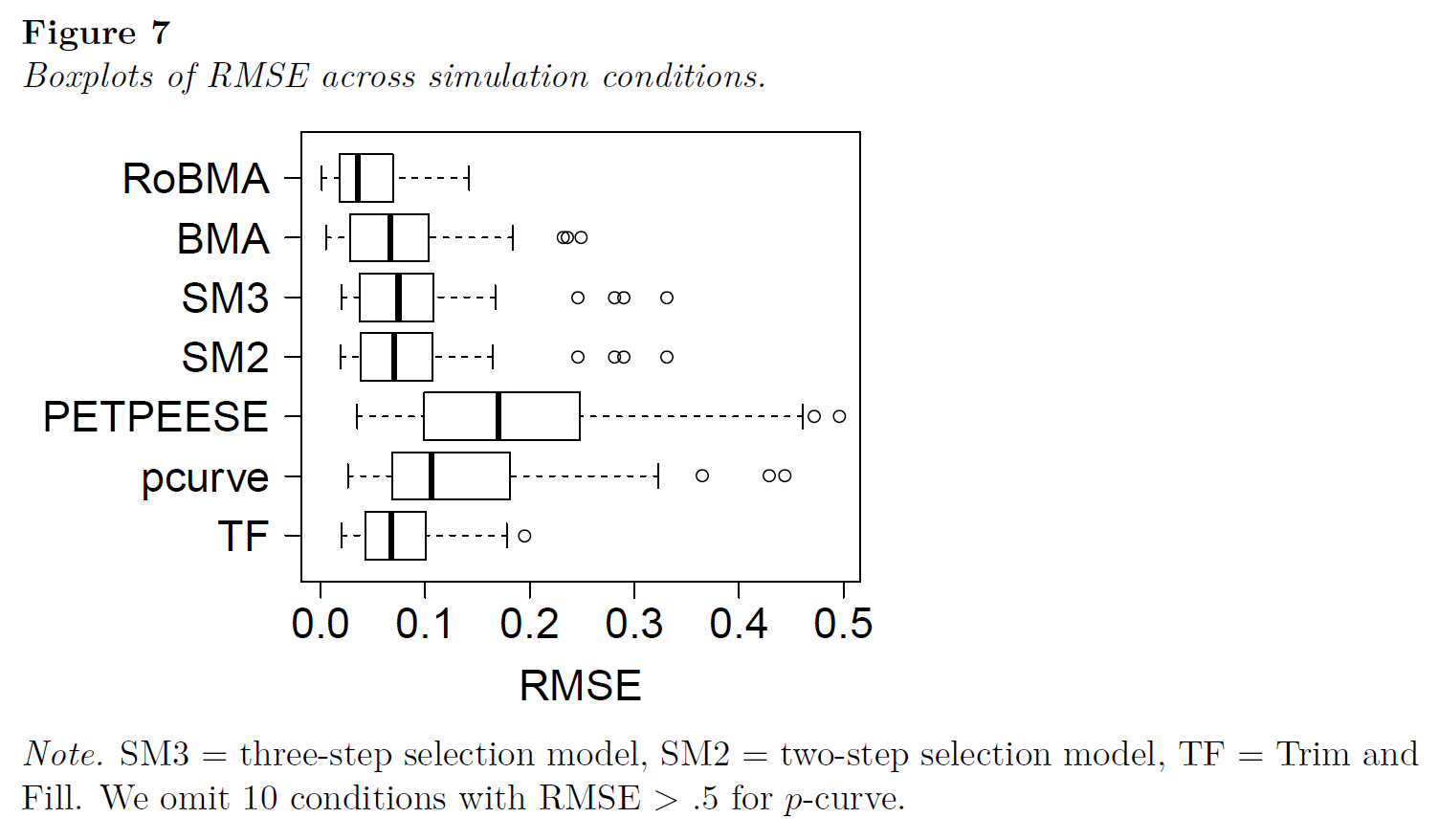
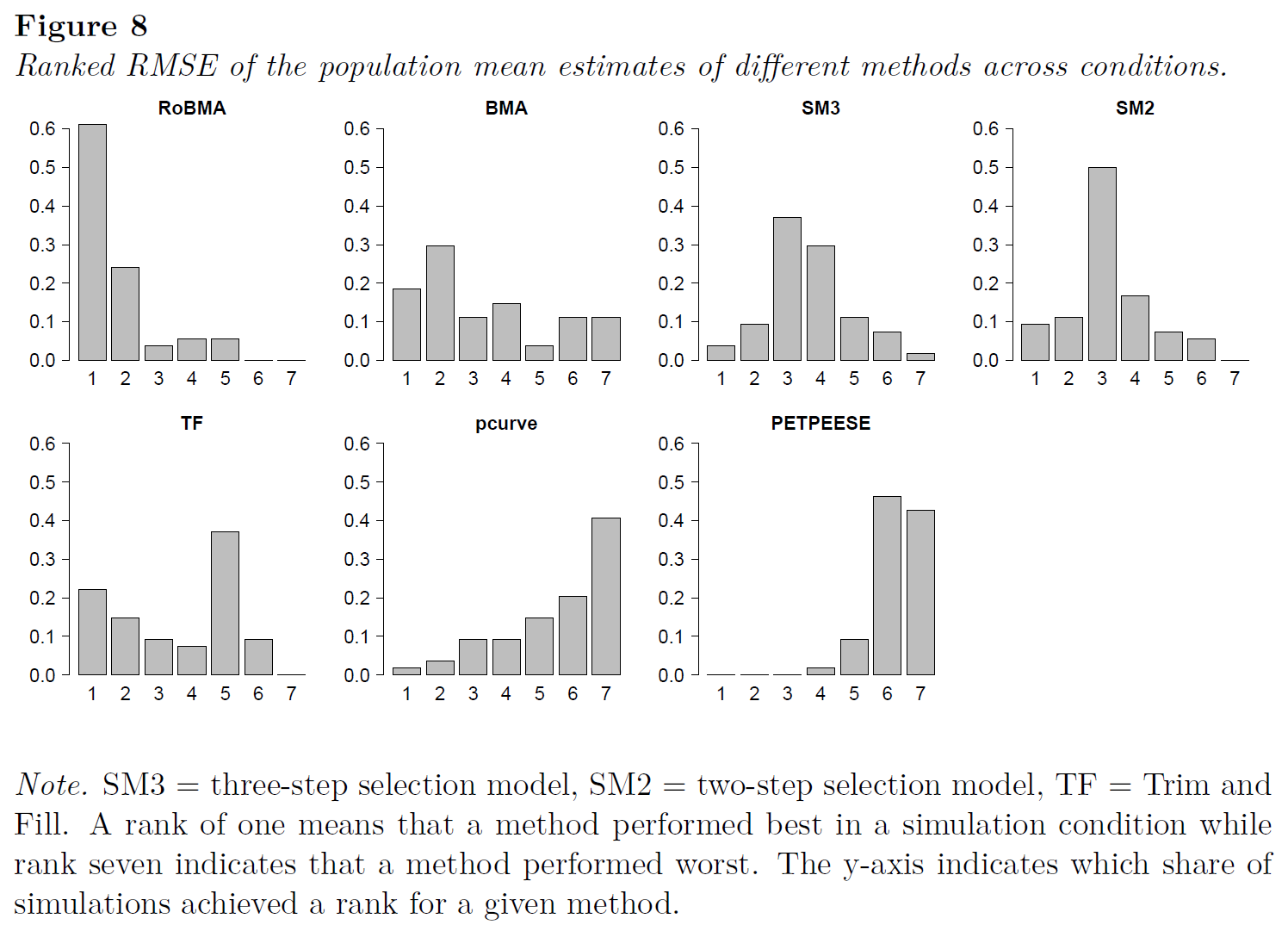
Simulation Study
Concluding Comments
“In this paper we introduced a robust Bayesian meta-analysis that model-averages over selection models as well as fixed and random effects models. By applying a set of twelve models simultaneously our method respects the underlying uncertainty when deciding between different meta-analytical models and is comparatively robust to model misspecification. RoBMA also performs well in different simulation conditions and correctly finds support for the absence of publication bias in the Many Labs 2 example. Besides this ability to quantify the evidence for absence of publication bias, the Bayesian approach also allows to update evidence sequentially as studies accumulate, addressing recent concerns about accumulation bias (ter Schure & Grünwald, 2019).”
“To conclude, this work offers applied researchers a new, conceptually straightforward method to conduct meta-analysis. Instead of basing conclusions on a single model, our method is based on keeping all models in play, with the data determining model importance according to predictive success. The simulations and the example suggest that RoBMA is a promising new method in the toolbox of various approaches to test and adjust for publication bias in meta-analysis.”
References
Maier, M., Bartoš, F. & Wagenmakers. E.-J. (2020). Robust Bayesian meta-analysis: Addressing publication bias with model-averaging. https://psyarxiv.com/u4cns
About The Authors

Maximilian Maier
Maximilian Maier is a Research Master student in psychology at the University of Amsterdam.

František Bartoš
František Bartoš is a Research Master student in psychology at the University of Amsterdam.

Eric-Jan Wagenmakers
Eric-Jan (EJ) Wagenmakers is professor at the Psychological Methods Group at the University of Amsterdam.