This post is an extended synopsis of Stefan, A. M., Evans, N. J., & Wagenmakers, E.-J. (2019). Practical challenges and methodological flexibility in prior elicitation. Manuscript submitted for publication. Preprint available on PsyArXiv: https://psyarxiv.com/d42xb/

 
 
 

Abstract

It is a well-known fact that Bayesian analyses require the specification of a prior distribution, and that different priors can lead to different quantitative, or even qualitative, conclusions. Because the prior distribution can be so influential, one of the most frequently asked questions about the Bayesian statistical framework is: How should I specify the prior distributions? Here, we take a closer look at prior elicitation — a subjective Bayesian method for specifying (informed) prior distributions based on expert knowledge — and examine the practical challenges researchers may face when implementing this approach for specifying their prior distributions. Specifically, our review of the literature suggests that there is a high degree of methodological flexibility within current prior elicitation techniques. This means that the results of a prior elicitation effort are not solely determined by the expert’s knowledge, but also heavily depend on the methodological decisions a researcher makes in the prior elicitation process. Thus, it appears that prior elicitation does not completely solve the issue of prior specification, but instead shifts influential decisions to a different level. We demonstrate the potential variability resulting from different methodological choices within the prior elicitation process in several examples, and make recommendations for how the variability in prior elicitation can be managed in future prior elicitation efforts.

What Is Prior Elicitation?

Prior distributions are probability distributions that reflect knowledge about the relative plausibility of different parameter values before analysing the current sample of data. Prior elicitation is an approach for specifying prior distributions based on the knowledge of field experts. Typically, prior elicitation consists of a structured interview, in which an interviewer guides one or more field experts through the process of expressing their knowledge in a probabilistic form. Usually this involves experts formulating their knowledge into quantiles (e.g., tertiles or quartiles), which are intended to reflect their internal probability distribution for these parameters. These elicited quantities can then be used to construct a probability distribution that serves as a prior distribution in the Bayesian model. If more than one expert participated in the prior elicitation, their elicited distributions can be combined into one aggregated prior distribution.

Methodological Decisions In Prior Elicitation

Even though prior elicitation is an appealing approach for determining prior distributions in practical applications, we find that it also comes with several practical challenges. Specifically, researchers need to make multiple decisions at different stages of the elicitation process, which each provide important researcher degrees of freedom. Some of these decisions are depicted below and split into three categories: Decisions about the setup of the prior elicitation, decisions about the elicitation process itself, and decisions about the combination of priors from different experts.

How Do Methodological Decisions Influence the Results of Prior Elicitations?

Here, we show two examples of how different methodological decisions can shape the results of a prior elicitation procedure. Notably, in both cases we consider the exact same set of elicited quantiles, which can lead to greatly varying priors depending on the researcher’s decision. In our preprint (https://psyarxiv.com/d42xb/), we provide more examples of potentially influential methodological decisions, and discuss the effects of specific decisions in more detail.

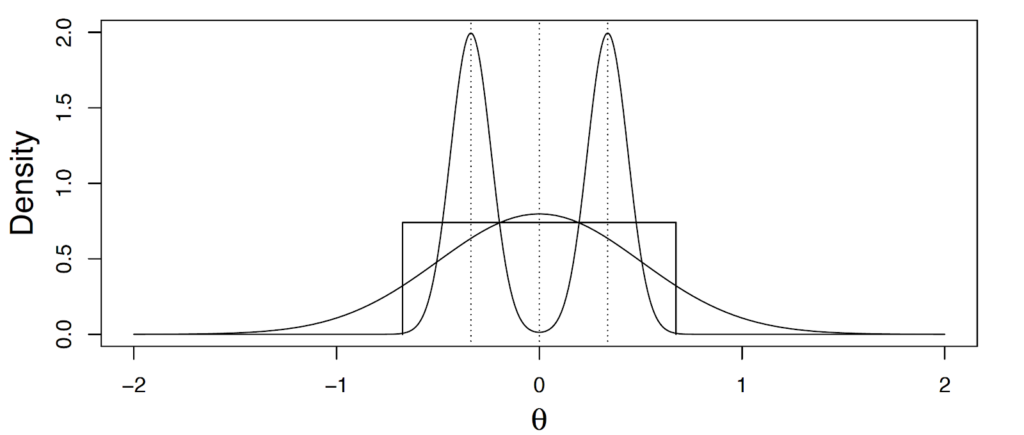
Example 1: What functional form should be used to fit the prior?

Suppose that a researcher used the so-called Quartile Method to elicit a prior distribution from an expert. In this prior elicitation technique, experts are asked to provide the 25th, 50th, and 75th percentile of their personal probability distribution on parameters. It is then up to the researcher to derive a probability distribution from the three elicited quantities. However, as can be seen from the figure below, three quantiles are not sufficient to uniquely identify a probability distribution. Different candidate distributions can fit equally well to the elicited quantiles, and therefore, the researcher needs to make additional assumptions (e.g., about the distributional family) to determine the prior distribution. As in the figure below, these additional assumptions eventually determine the shape of the prior distribution and constitute an important source of flexibility in the prior elicitation process.

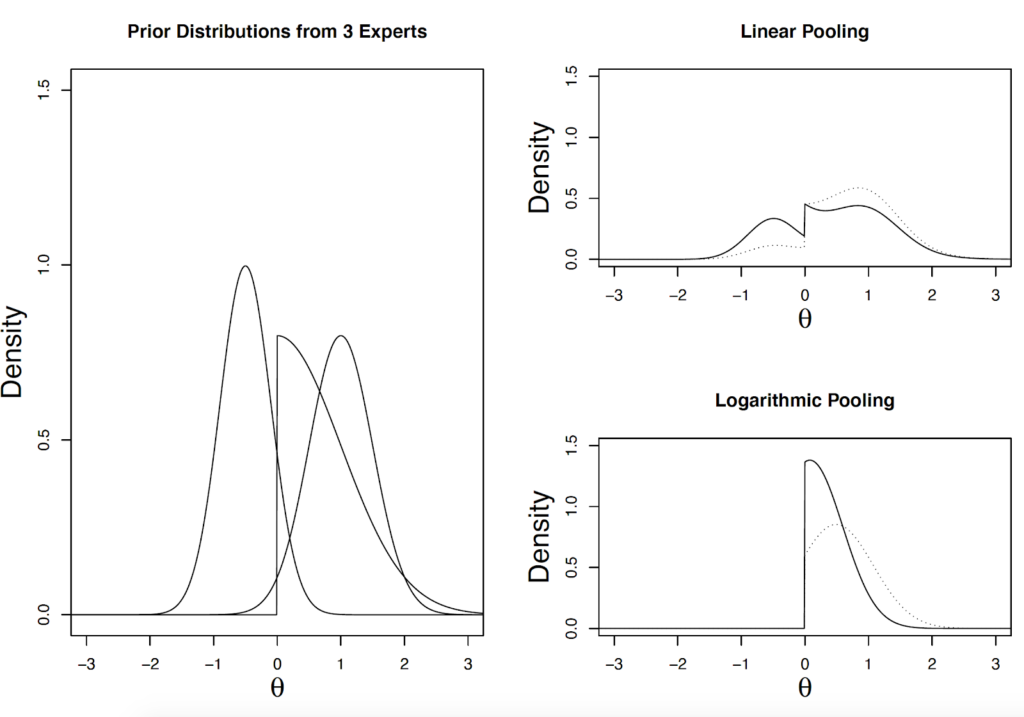
Example 2: How to combine prior distributions from different experts?

When it comes to complex problems, there are often as many opinions as there are experts. Therefore, it seems intuitively sensible to integrate knowledge from multiple experts into the prior distribution, that is, to elicit prior distributions from multiple experts and combine them to a single prior distribution. However, combining two or more probability distributions can be challenging in practice because researchers can choose from a variety of aggregation methods that can lead to highly different results. Here, we will only show two simple examples: linear and logarithmic pooling. In linear pooling methods, the resulting prior is a weighted average of the experts’ distributions. In logarithmic pooling methods, the experts’ distributions are combined with a weighted multiplicative mixture. As can be seen in the example in the figure below, linear pooling results in a wide multimodal prior distribution, whereas logarithmic pooling results in a more condensed unimodal distribution. Additionally, logarithmic pooling provides single experts with the ability to eliminate information from other experts, as any parameter value that a single expert classes as impossible (i.e., a probability density of 0) will also be classed as impossible in the aggregated distribution. The weight assigned to each expert’s distribution — which can be thought of as the relative importance that the researcher assigns to the information provided by each expert — also clearly influences the resulting prior distribution (see the dotted lines in the figure below). Thus, the freedom to choose a specific setup of the pooling method allows researchers to specify qualitatively different prior distributions based on identical elicited prior distributions for each expert.

Conclusion

The above examples show that researchers’ methodological decisions in prior elicitation matter. However, the current literature on prior elicitation mostly neglects this issue. As in other research areas, hidden researcher degrees of freedom can compromise the principled nature of an approach when researchers are incentivized to abuse them. Therefore, we argue that transparency is important to maintain the credibility and methodological rigor of the prior elicitation process. Furthermore, transparency about methodological decisions may spur new developments in the field of prior elicitation. For example, acknowledging the multiplicity of outcomes in prior elicitation can inspire new forms of prior robustness analyses that are based on the multiple outcomes of a prior elicitation procedure. Moreover, making decisions in prior elicitation transparent can shed more light on the elicitation process itself. Are some decisions better than others? What effects do they actually have on the results? How can researchers justify the decisions within the prior elicitation procedure? Importantly, the first step to answering these questions is to explicitly highlight the different methodological decisions in prior elicitation; something we have aimed to do both here and within our preprint (https://psyarxiv.com/d42xb/).

To conclude, we believe that undocumented methodological decisions within the prior elicitation process make informed Bayesian methods an easy target of criticism. Thus, acknowledging the practical methodological flexibility in prior elicitation can contribute to a constructive advance of the debate about prior specification in Bayesian methods.

About The Authors

Angelika Stefan

Angelika is a PhD candidate at the Psychological Methods Group of the University of Amsterdam.

Nathan Evans

Nathan Evans is a postdoc at the Psychological Methods Group at the University of Amsterdam.

Eric-Jan Wagenmakers

Eric-Jan (EJ) Wagenmakers is professor at the Psychological Methods Group at the University of Amsterdam.