Preprint: https://psyarxiv.com/5ntkd

Abstract

“Is it statistically appropriate to monitor evidence for or against a hypothesis as the data accumulate, and stop whenever this evidence is deemed sufficiently compelling? Researchers raised in the tradition of frequentist inference may intuit that such a practice will bias the results and may even lead to “sampling to a foregone conclusion”. In contrast, the Bayesian formalism entails that the decision on whether or not to terminate data collection is irrelevant for the assessment of the strength of the evidence. Here we provide five Bayesian intuitions for why the rational updating of beliefs ought not to depend on the decision when to stop data collection, that is, for the Stopping Rule Principle.”

Fragment: Only One Creature Cares About The Stopping Rule

“Crucially, at no point during the investigation would a detective take into account the stopping rule in order to adjust his assessment of the evidence. This utter disregard for the stopping rule is not unique to detectives solving murder mysteries; it was also on display, for instance, in Thorndike’s cats when they sought to escape his puzzle boxes; it was there in the alphaGo program when it taught itself to play Go; it is present in the spam filters that make email a usable technology; and it is evident in children who learn to speak. For their survival, almost all living creatures need to update their knowledge based on a continual stream of feedback from the environment. No real-life learner has ever given a moment’s thought as to how a stopping rule ought to adjust the evidence obtained thus far. The only organisms who seem to care about stopping rules are frequentist statisticians.”

Pythagoras Meets Bayes

Bayes’ theorem “is to the theory of probability what Pythagoras’ theorem is to geometry” (Jeffreys, 1931, p. 19).

Specific Forms of Model Misspecification May Cause Trouble

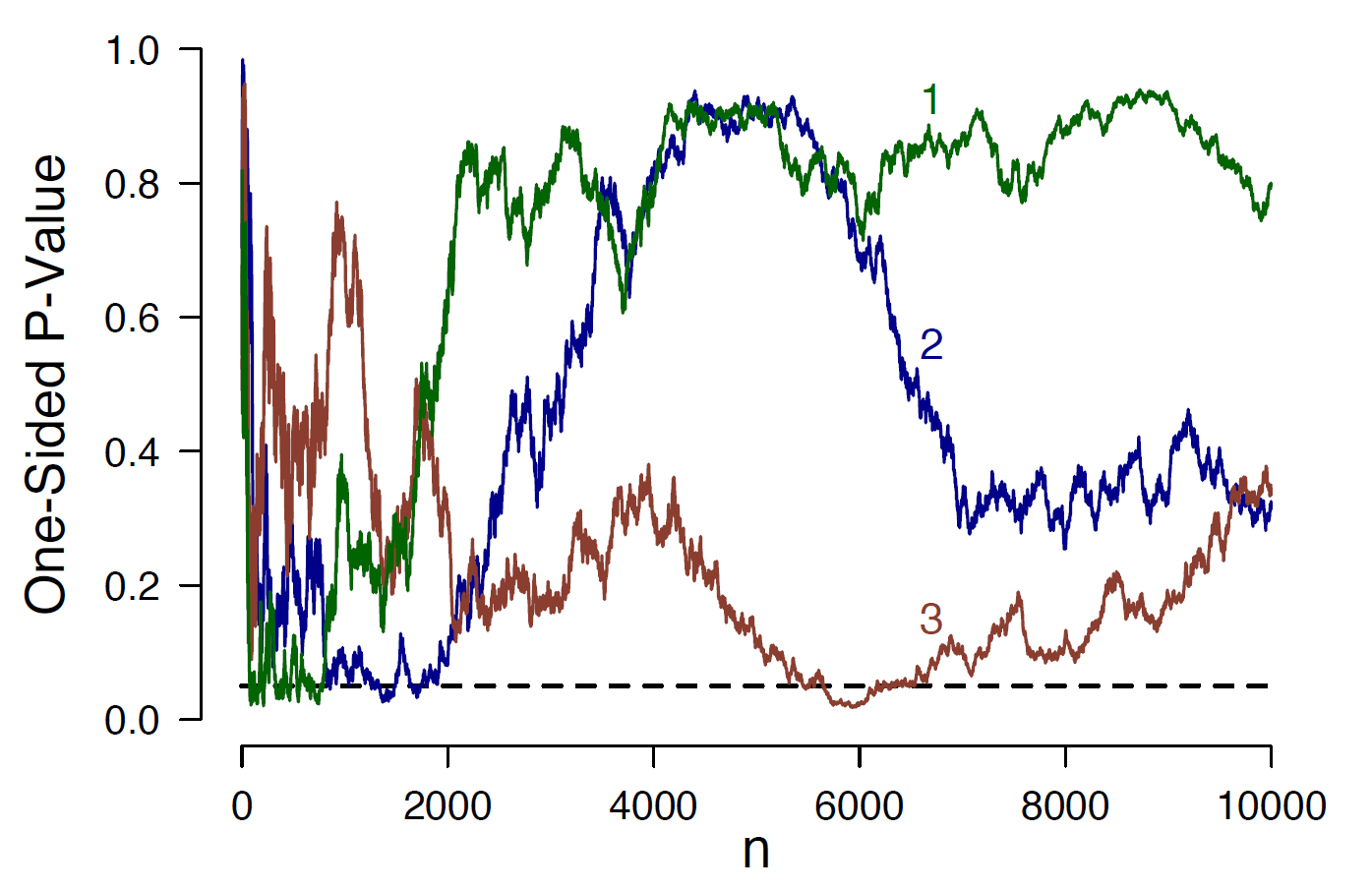
Below are three different data sets: green (“1”), blue (“2”), and red (“3”). Each data set is generated under the null hypothesis of no effect. In the first panel below, we see how the p-value (the one-sided p-value, in this case) meanders randomly, such that a sufficiently patient researcher could simply wait until a significant outcome is obtained (hence the moniker “sampling to a foregone conclusion”).

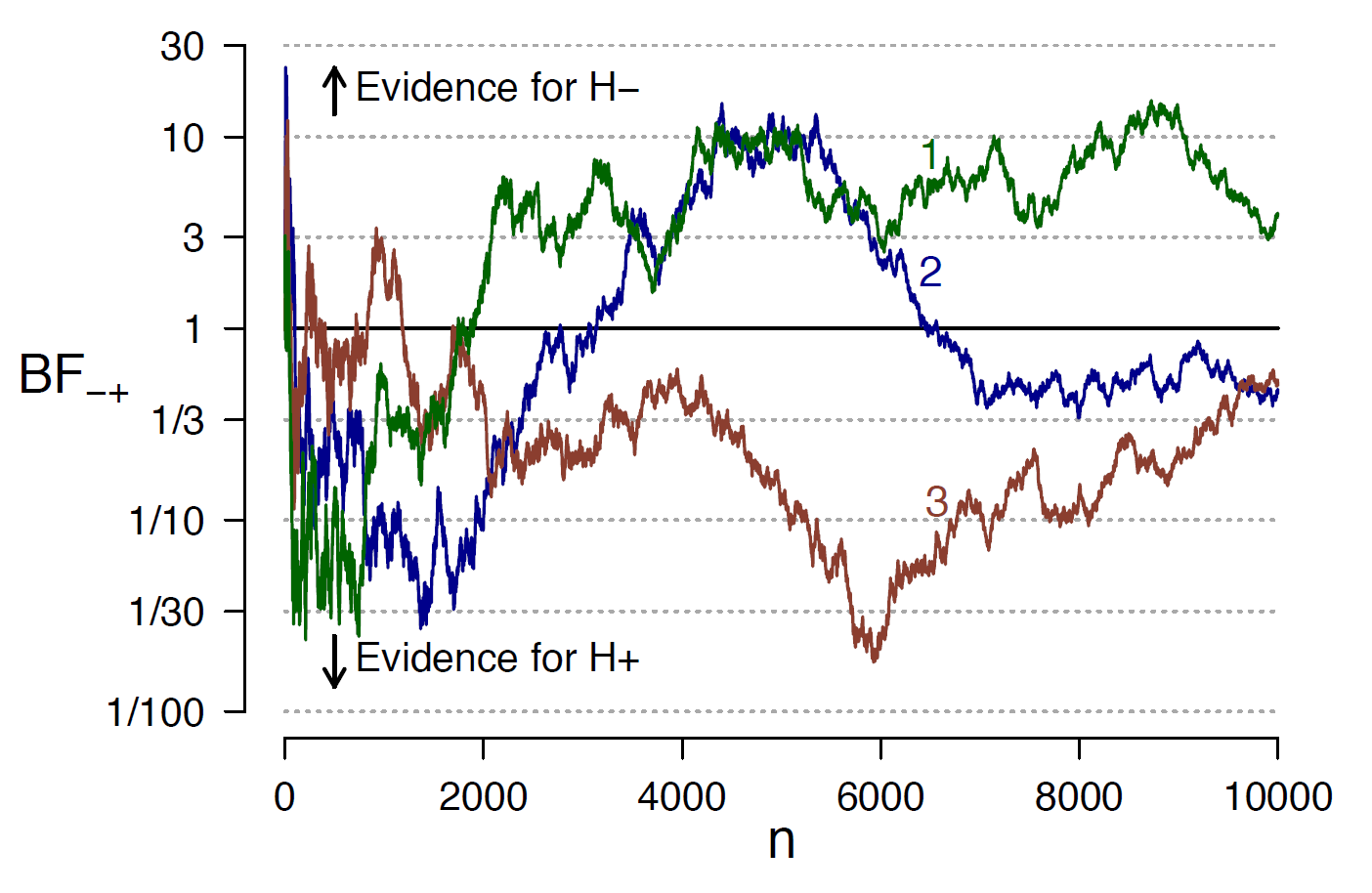
The next panel shows, for exactly the same three data sets, the outcome of a Bayes factor test for directionality, that is, contrasting the hypothesis that the effect is negative against the hypothesis that it is positive. Note that the true effect is exactly in the middle, so that neither of the two hypotheses is true, and both are equally far removed from the truth. Just as the p-value, the Bayes factor for directionality also meanders randomly and is hence subject to “sampling to a foregone conclusion”.

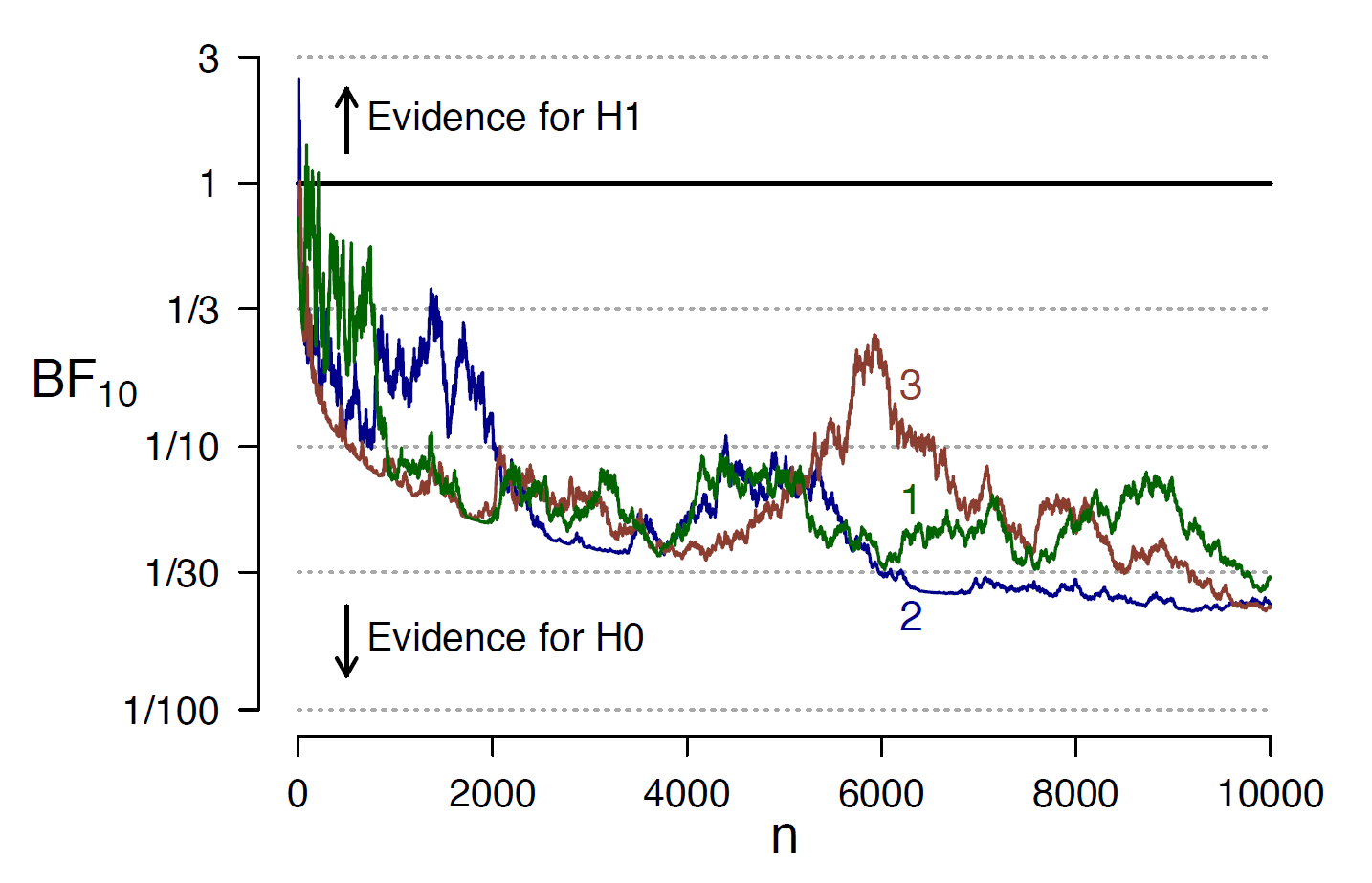
The final panel shows, again for exactly the same three data sets, the outcome of a Bayes factor test that compares the null hypothesis against an alternative hypothesis. Because the null hypothesis generated the data, the Bayes factor indicates increasing support for the null as sample size increases. A researcher who intends to wait until the evidence supports the incorrect alternative hypothesis is likely to wait in vain.

References

Jeffreys, H. (1931). Scientific inference (1st ed.). Cambridge, UK: Cambridge University Press.

Wagenmakers, E.-J., Gronau, Q. F., & Vandekerckhove, J. (2019). Five Bayesian intuitions for the stopping rule principle. Manuscript posted on PsyArXiv. https://psyarxiv.com/5ntkd

About The Authors

Eric-Jan Wagenmakers

Eric-Jan (EJ) Wagenmakers is professor at the Psychological Methods Group at the University of Amsterdam.

Quentin Gronau

Quentin is a PhD candidate at the Psychological Methods Group of the University of Amsterdam.

Joachim Vandekerckhove

Joachim Vandekerckhove is an Associate Professor at the University of California.