This post is a synopsis of Bartoš et al. (2023). Fair coins tend to land on the same side they started: Evidence from 350,757 flips. Preprint available at https://doi.org/10.48550/arXiv.2310.04153. Post-specific images were generated by Bing.

Abstract

Many people have flipped coins but few have stopped to ponder the statistical and physical intricacies of the process. In a preregistered study we collected 350,757 coin flips to test the counterintuitive prediction from a physics model of human coin tossing developed by Diaconis, Holmes, and Montgomery (D-H-M; 2007). The model asserts that when people flip an ordinary coin, it tends to land on the same side it started — D-H-M estimated the probability of a same-side outcome to be about 51%. Our data lend strong support to this precise prediction: the coins landed on the same side more often than not, Pr(same side)=0.508, 95% credible interval (CI) [0.506, 0.509], BF_{same-side bias}= 2364. Furthermore, the data revealed considerable between-people variation in the degree of this same-side bias. Our data also confirmed the generic prediction that when people flip an ordinary coin — with the initial side-up randomly determined — it is equally likely to land heads or tails: Pr(heads)=0.500, 95% CI [0.498, 0.502], BF_{heads-tails bias}=0.183. Furthermore, this lack of heads-tails bias does not appear to vary across coins. Our data therefore provide strong evidence that when some (but not all) people flip a fair coin, it tends to land on the same side it started. Our data provide compelling statistical support for the D-H-M physics model of coin tossing.

350,757 Flips

About a year ago, we embarked on a quest to answer one of Nature’s most pressing questions:

If you flip a fair coin and catch it in your hand, what is the probability it lands on the same side that it started?

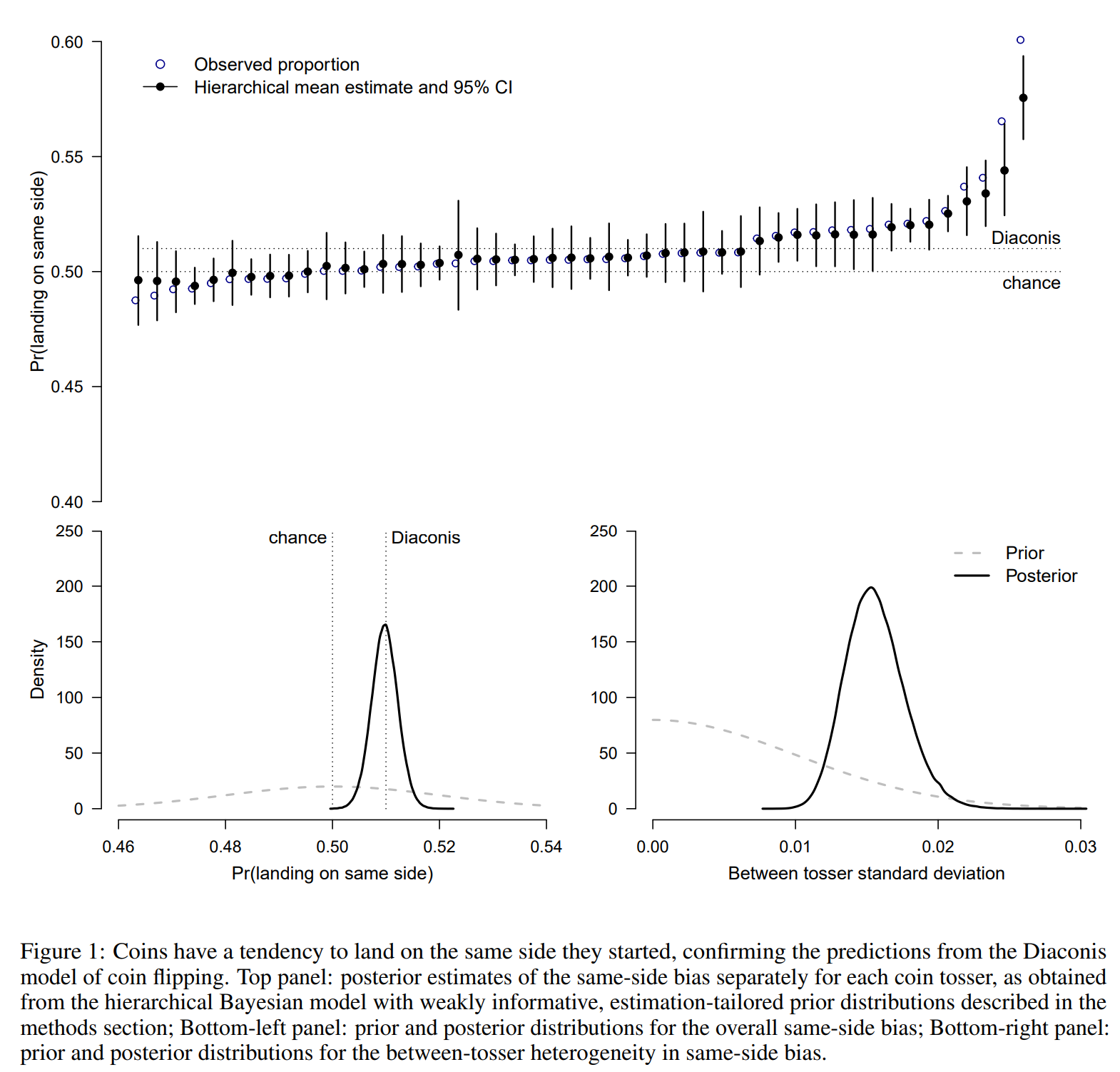
Today, we are finally ready to share the results. Thanks to our friends, collaborators, and even strangers from the internet, we collected to total of 350,757 coin flips. We ran several “Coin Tossing Marathons” (e.g., https://youtu.be/3xNg51mv-fk?si=o2E3hKa-ReXodOmc) and spent countless hours flipping coins. Our results reveal overwhelming evidence for the “same-side” bias predicted by Diaconis, Holmes, and Montgomery (D-H-M) in 2007: If you start heads-up, the coin is more likely to land heads-up and vice versa. How large is the bias? In our sample, the mean estimate is 50.8%, CI [50.6%, 50.9%], remarkably close to the prediction from D-H-M, which was “about .51”.

If you bet a dollar on the outcome of a coin toss 1000 times, knowing the starting position of the coin toss would earn you 19 dollars on average. This is more than the casino advantage for 6-deck blackjack against an optimal player (5 dollars) but less than that for single-zero roulette (27 dollars).

We also found considerable variance in the same-side bias between our 48 tossers. The bias varied with a standard deviation of 1.6%, CI [1.2%, 2.0%], in our sample. The variation might be due to a different degree of  “wobbliness” between our tossers.

The manuscript is at arXiv: https://arxiv.org/abs/2310.04153, and the open data, code, and video recordings are at OSF: https://osf.io/pxu6r/.

References

Bartoš et al. (2023). Fair coins tend to land on the same side they started: Evidence from 350,757 flips. Preprint available at https://doi.org/10.48550/arXiv.2310.04153

Diaconis, P., Holmes, S., & Montgomery, R. (2007). Dynamical bias in the coin toss. SIAM Review, 49(2), 211-235. https://doi.org/10.1137/S0036144504446436.

About The Author

Frantisek Bartos

František Bartoš is a PhD candidate at the Psychological Methods Group of the University of Amsterdam.