This post is an extended synopsis of Linde, M., Tendeiro, J. N., Selker, R., Wagenmakers, E.-J., & van Ravenzwaaij, D. (submitted). Decisions about equivalence: A comparison of TOST, HDI-ROPE, and the Bayes factor. Preprint available on PsyArXiv: https://psyarxiv.com/bh8vu
Abstract
Some important research questions require the ability to find evidence for two conditions being practically equivalent. This is impossible to accomplish within the traditional frequentist null hypothesis significance testing framework; hence, other methodologies must be utilized. We explain and illustrate three approaches for finding evidence for equivalence: The frequentist two one-sided tests procedure (TOST), the Bayesian highest density interval region of practical equivalence procedure (HDI-ROPE), and the Bayes factor interval null procedure (BF). We compare the classification performances of these three approaches for various plausible scenarios. The results indicate that the BF approach compares favorably to the other two approaches in terms of statistical power. Critically, compared to the BF procedure, the TOST procedure and the HDI-ROPE procedure have limited discrimination capabilities when the sample size is relatively small: specifically, in order to be practically useful, these two methods generally require over 250 cases within each condition when rather large equivalence margins of approximately 0.2 or 0.3 are used; for smaller equivalence margins even more cases are required. Because of these results, we recommend that researchers rely more on the BF approach for quantifying evidence for equivalence, especially for studies that are constrained on sample size.
Introduction
Science is dominated by a quest for effects. Does a certain drug work better than a placebo? Are pictures containing animals more memorable than pictures without animals? These attempts to demonstrate the presence of effects are partly due to the statistical approach that is traditionally employed to make inferences. This framework – null hypothesis significance testing (NHST) – only allows researchers to find evidence against but not in favour of the null hypothesis that there is no effect. In certain situations, however, it is worthwhile to examine whether there is evidence for the absence of an effect. For example, biomedical sciences often seek to establish equal effectiveness of a new versus an existing drug or biologic. The new drug might have fewer side effects and would therefore be preferred even if it is only as effective as the old one. Answering questions about the absence of an effect requires other tools than classical NHST. We compared three such tools: The frequentist two one-sided tests approach (TOST; e.g., Schuirmann, 1987), the Bayesian highest density interval region of practical equivalence approach (HDI-ROPE; e.g., Kruschke, 2018), and the Bayes factor interval null approach (BF; e.g., Morey & Rouder, 2011).
We estimated statistical power and the type I error rate for various plausible scenarios using an analytical approach for TOST and a simulation approach for HDI-ROPE and BF. The scenarios were defined by three global parameters:
- Population effect size: δ = {0,0.01,…,0.5}
- Sample size per condition: n = {50,100,250,500}
- Standardized equivalence margin: m = {0.1,0.2,0.3}
In addition, for the Bayesian approaches we placed a Cauchy prior on the population effect size with a scale parameter of r = {0.5/√2,1/√2,2/√2}. Lastly, for the BF approach specifically, we used Bayes factor thresholds of BFthr = {3,10}.
Results
The results for an equivalence margin of m = 0.2 are shown in Figure 1. The overall results for equivalence margins of m = 0.1 and m = 0.3 were similar and are therefore not shown here. Ideally, the proportion of equivalence decisions would be 1 when δ lies inside the equivalence interval and 0 when δ lies outside the equivalence interval. The results show that TOST and HDI-ROPE are maximally conservative to conclude equivalence when sample sizes are relatively small. In other words, these two approaches never make equivalence decisions, which means they have no statistical power but they also make no type I errors. With our choice of Bayes factor thresholds, the BF approach is more liberal to make equivalence decisions, displaying higher power but also a higher type I error rate. Although far from perfect, the BF approach has rudimentary discrimination abilities for relatively small sample sizes. As the sample size increases, the classification performances of all three approaches improve. In comparison to the BF approach, the other two approaches remain quite conservative.
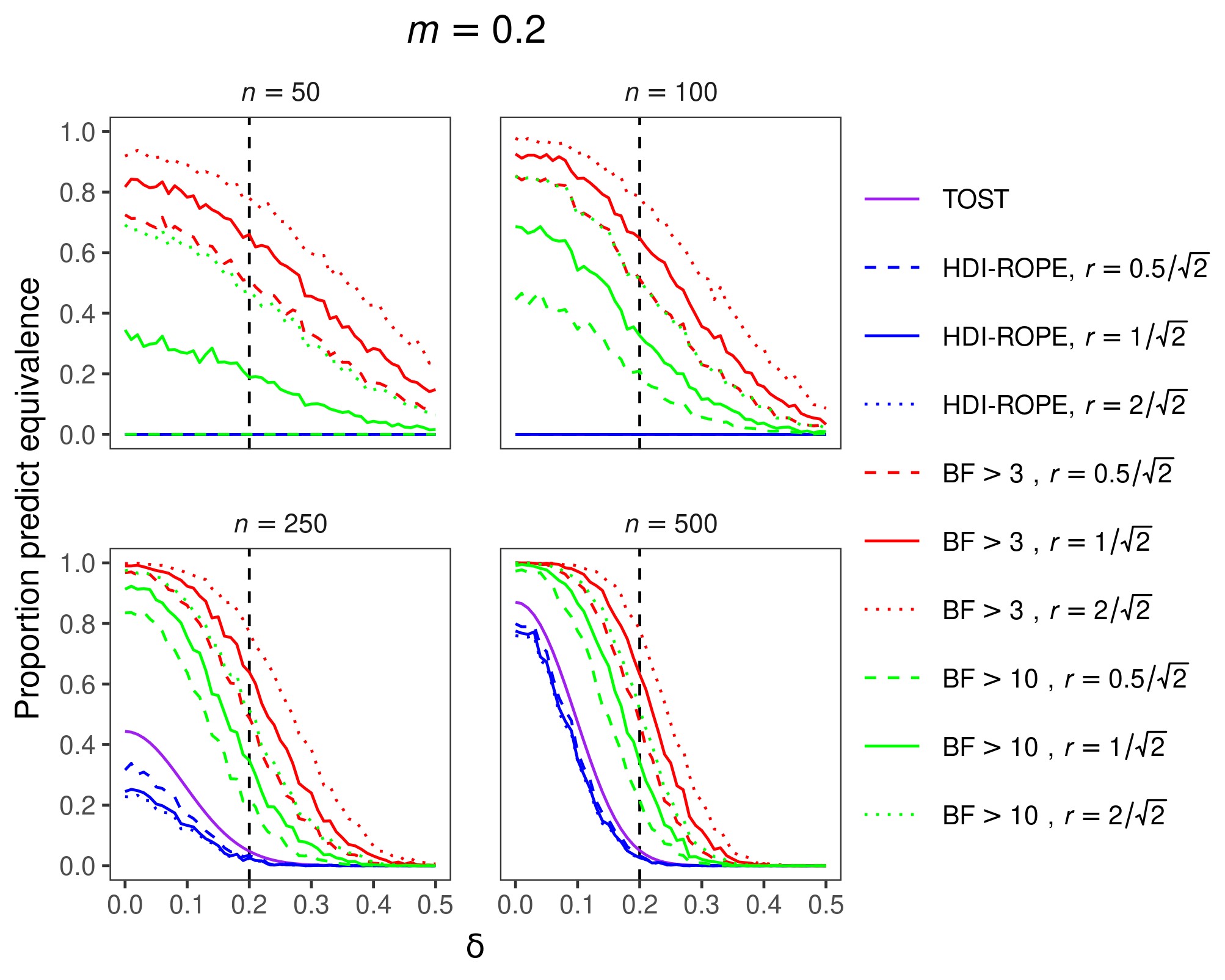Figure 1. Proportion of equivalence predictions with a standardized equivalence margin of m = 0.2. Panels contain results for different sample sizes. Colors denote different inferential approaches (and different decision thresholds within the BF approach). Line types denote different priors (for Bayesian metrics). Predictions of equivalence are correct if the population effect size (δ) lies within the equivalence interval (power), whereas predictions of equivalence are incorrect if δ lies outside the equivalence interval (Type I error rate).
Making decisions based on small samples should generally be avoided. If possible, more data should be collected before making decisions. However, sometimes sampling a relatively large number of cases is not feasible. In that case, the use of Bayes factors might be preferred because they display some discrimination capabilities. In contrast, TOST and HDI-ROPE are maximally conservative. For large sample sizes, all three approaches perform almost optimally when the population effect size is in the center of the equivalence interval or when it is very large (or low). However, the BF approach results in more balanced decisions at the decision boundary (i.e., where the population effect size is equal to the equivalence margin). In summary, we recommend the use of Bayes factors for making decisions about the equivalence of two groups.
References
Kruschke, J. K. (2018). Rejecting or accepting parameter values in Bayesian estimation. Advances in Methods and Practices in Psychological Science, 1(2), 270–280.
Morey, R. D., & Rouder, J. N. (2011). Bayes factor approaches for testing interval null hypotheses. Psychological Methods, 16(4), 406–419.
Schuirmann, D. J. (1987). A comparison of the two one-sided tests procedure and the power approach for assessing the equivalence of average bioavailability. Journal of Pharmacokinetics and Biopharmaceutics, 15(6), 657–680.
About The Authors
Maximilian Linde
Maximilian Linde is PhD student at the Psychometrics & Statistics group at the University of Groningen.
Jorge N. Tendeiro
Jorge N. Tendeiro is assistant professor at the Psychometrics & Statistics group at the University of Groningen.
Ravi Selker
Ravi Selker was PhD student at the Psychological Methods group at the University of Amsterdam (at the time of involvement in this project).
Eric-Jan Wagenmakers
Eric-Jan (EJ) Wagenmakers is professor at the Psychological Methods Group at the University of Amsterdam.
Don van Ravenzwaaij
Don van Ravenzwaaij is associate professor at the Psychometrics & Statistics group at the University of Groningen.
