Recently I was involved in an Email correspondence where someone claimed that Bayes factors always involve a point null hypothesis, and that the point null is never true — hence, Bayes factors are useless, QED. Previous posts on this blog here and here discussed the scientific relevance (or even inevitability?) of the point null hypothesis, but the deeper problem with the argument is that the premise is false. Bayes factors compare the predictive performance of any two models; one of the models may be a point-null hypothesis, if this is deemed desirable, interesting, or scientifically relevant; however, instead of the point-null you can just as well specify a Tukey peri-null hypothesis, an interval-null hypothesis, a directional hypothesis, or a nonnested hypothesis. The only precondition that needs to be satisfied in order to compute a Bayes factor between two models is that the models must make predictions (see also Lee & Vanpaemel, 2018).

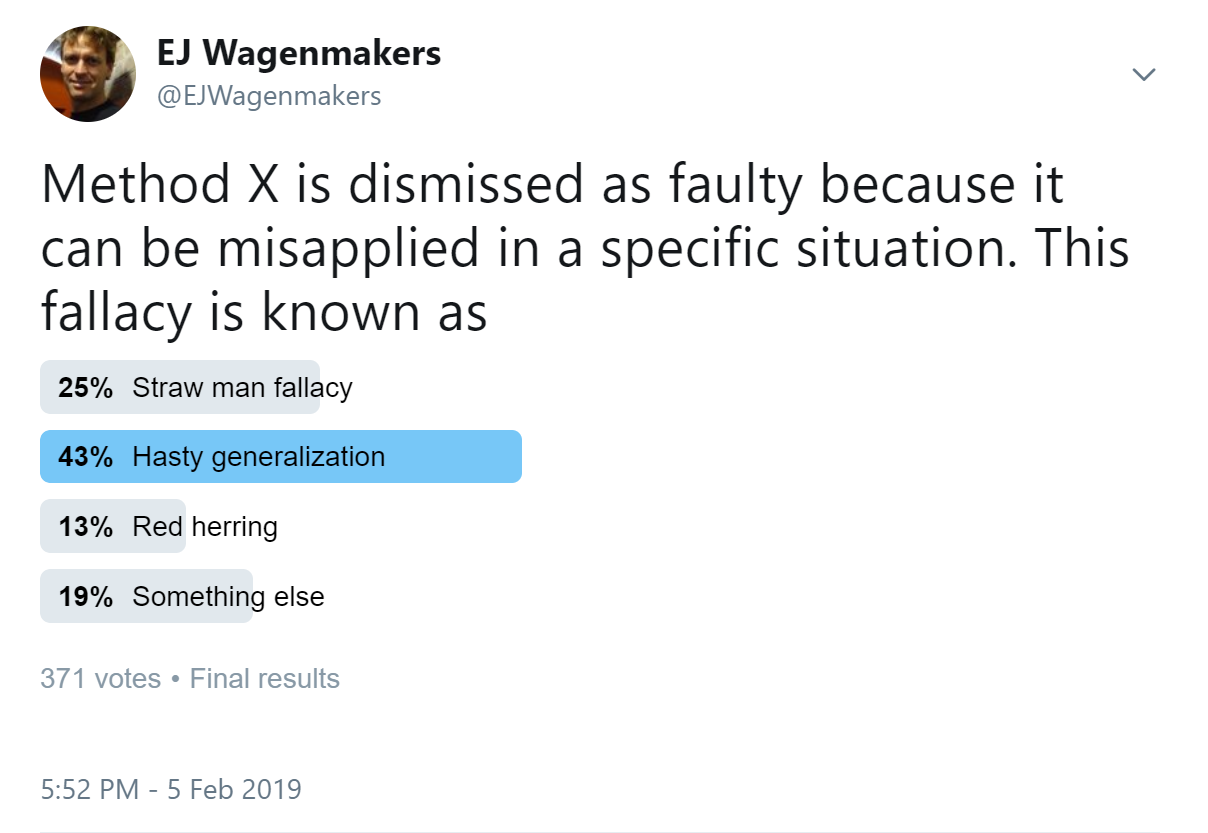
I have encountered a similar style of reasoning before, and I was wondering how to classify this fallacy. So I ran the following poll on twitter:

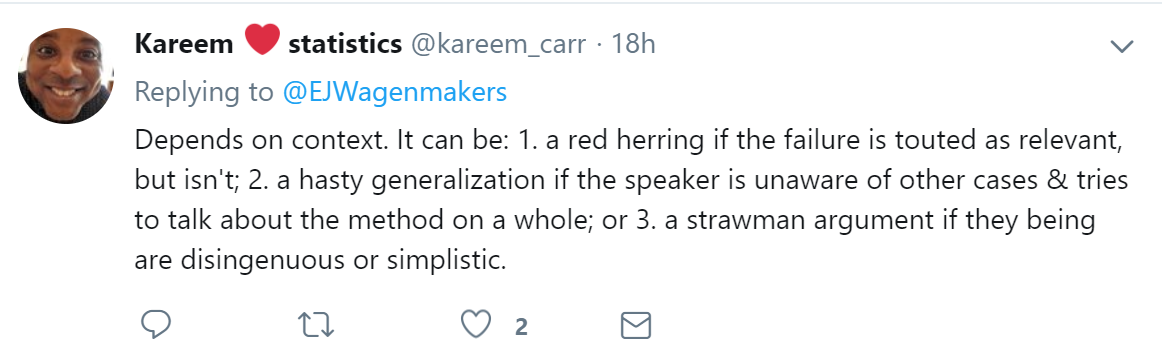
So there is some disagreement, although “hasty generalization” is a clear favorite (no I’m not going to run a statistical test on these data :-)). The responses I received were quite helpful. For instance, @kareem_carr suggested that it depends on context:

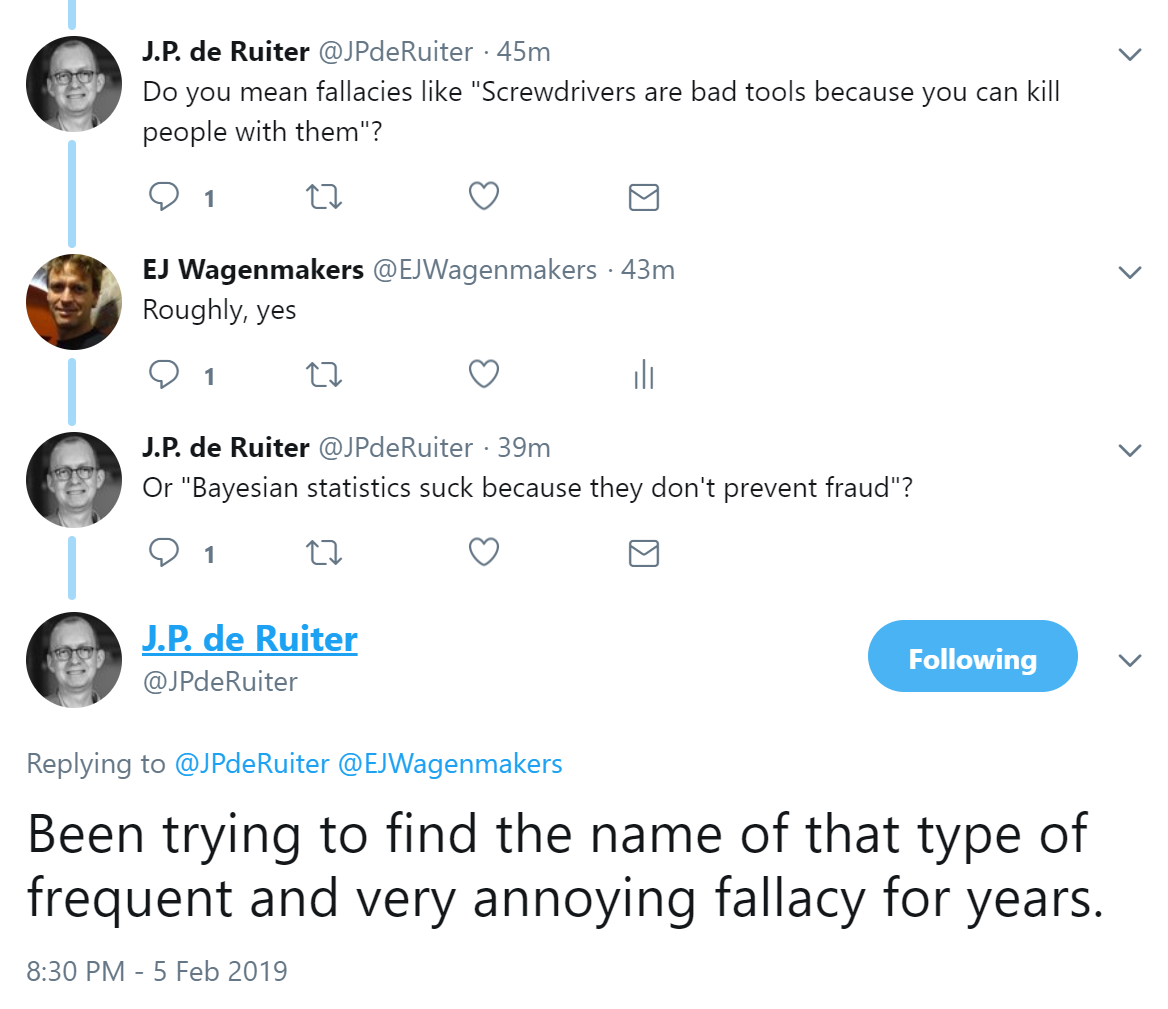
Then, @JPdeRuiter suggested that the proposed scenario was of the kind “screwdrivers ought to be banned because they can be used for killing people”:

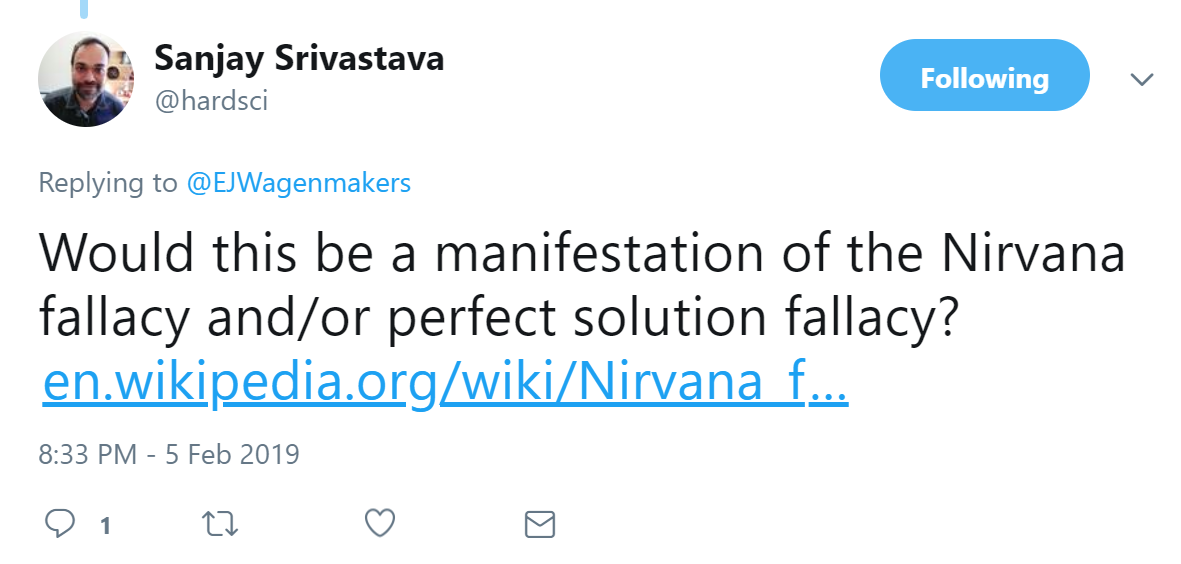
@hardsci argued that this was a case of the Nirvana fallacy:

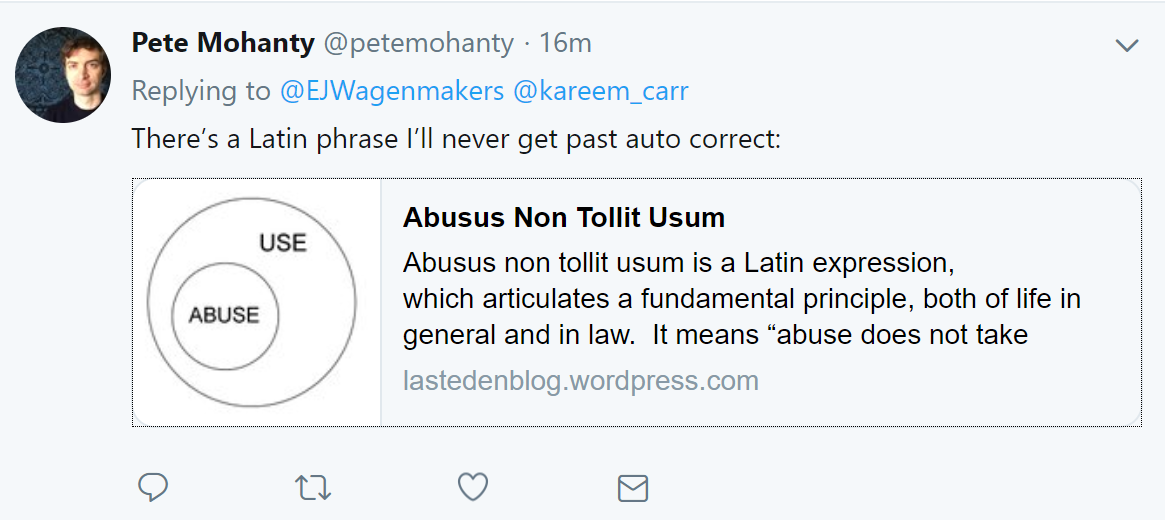
With respect to JPs example, @petemohanty absolutely nailed it: Abusus non tollit usum

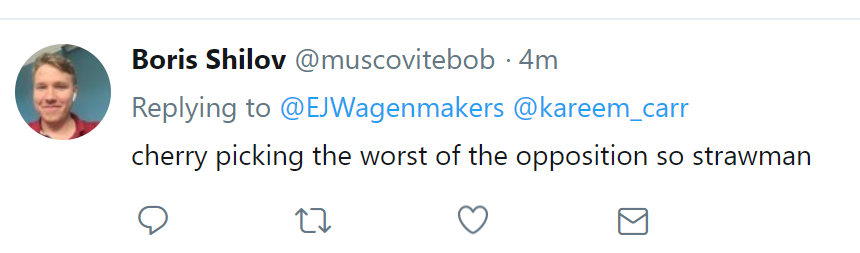
Another fallacy that could be relevant is cherry-picking, which was suggested by @muscovitebob:

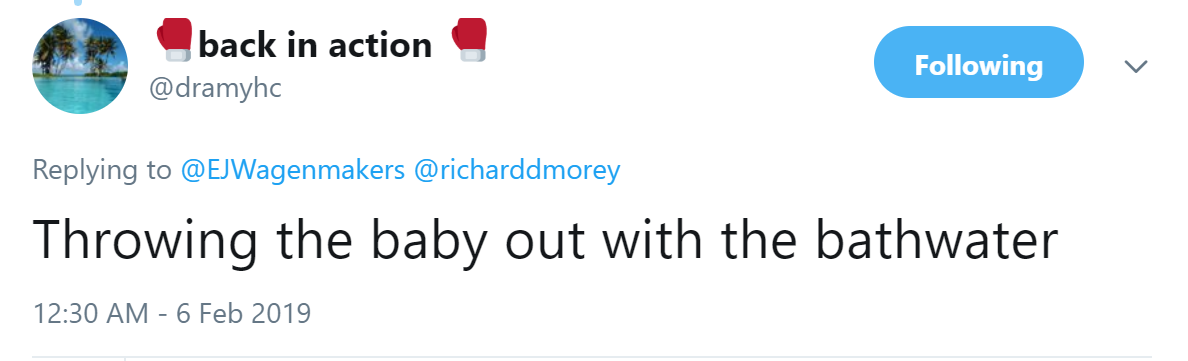
Finally, @dramyhc suggested another one:

And so did @OlegUrminsky:

The Oven

Bayesian pioneer Harold Jeffreys believed the statistical literature in the early 1900s presented a fallacy similar to the one discussed above: Bayesian inference (then known as “inverse probability”) always involves uniform priors; uniform priors are undesirable; Bayesian inference is undesirable, QED. In response, Jeffreys (1961, p. 118) presented a compelling analogy:

“Bayes and Laplace, having got so far, unfortunately stopped there, and the weight of their authority seems to have led to the idea that the uniform distribution of the prior probability was a final statement for all problems whatever, and also that it was a necessary part of the principle of inverse probability. There is no more need for the latter idea than there is to say that an oven that has once cooked roast beef can never cook anything but roast beef.” (Jeffreys, 1961, p. 118, emphasis added)

In a single sentence, this analogy strikes at the heart of the fallacy. The blame for a poorly cooked meal should not go to the oven (Bayes’ rule), but to the cook (the model specification). Also, there are still situations that call for a particular model (roast beef) — it is just not something most people would want to eat every day of the week. Finally, the analogy also suggests that, if we prefer a different dish, it would be best to have a good conversation with the cook instead of replacing the oven.

A final thought: ironically, it was perhaps the weight of Jeffreys’s authority that gave rise to the idea that Bayes factors need always involve a point null hypothesis…

References

Jeffreys, H. (1961). Theory of Probability (3rd ed.). Oxford: Oxford University Press.

Lee, M. D. & Vanpaemel, W. (2018). Determining informative priors for cognitive models. Psychonomic Bulletin & Review, 25, 114-127.

About The Author

Eric-Jan Wagenmakers

Eric-Jan (EJ) Wagenmakers is professor at the Psychological Methods Group at the University of Amsterdam.