Bayesian Scepsis About SWEPIS: Quantifying the Evidence That Early Induction of Labour Prevents Perinatal Deaths

July 09 - 2020

To paraphrase Mark Twain: “to someone with a hammer, everything looks like a nail”. And so, having implemented the Bayesian A/B test (Kass & Vaidyanathan, 1992) in R and in JASP (Gronau, Raj, & Wagenmakers, 2019), we have been on a mission to apply the methodology to various clinical trials. In contrast to most psychology experiments, lives are actually on the line in clinical trials, and we believe our Bayesian A/B test offers insights over and above the usual “ $p<.05$ , the treatment effect is present” and “ $p>.05$ , the treatment effect is absent”. A collection of these brief Bayesian reanalyses can be found here.

Apart from the merits and demerits of our specific analysis, it strikes us as undesirable that important clinical trials are analyzed in only one way — that is, based on the efforts of a single data-analyst, who operates within a single statistical framework, using a single statistical test, drawing a specific set of all-or-none conclusions. Instead, it seems prudent to present, alongside the original article, a series of brief comments that contain alternative statistical analyses; if these confirm the original result, this inspires trust in the conclusion; if these alternative analyses contradict the original result, this is grounds for caution and a deeper reflection on what the data tell us. Either way, we learn something important that we did not know before.

Anyhow, the latest installment in our collection concerns a Bayesian reanalysis of the SWEPIS clinical trial. The preprint is Wagenmakers & Ly, 2020 and its contents are copied below.

Bayesian Scepsis About SWEPIS

In a recent randomized clinical trial, Wennerholm and colleagues (2019) compared induction of labour at 41 weeks with expectant management and induction at 42 weeks. The primary endpoint was defined as “a composite perinatal outcome including one or more of stillbirth, neonatal mortality, Apgar score less than 7 at five minutes, pH less than 7.00 or metabolic acidosis (pH <7.05 and base deficit >12 mmol/L) in the umbilical artery, hypoxic ischaemic encephalopathy, intracranial haemorrhage, convulsions, meconium aspiration syndrome, mechanical ventilation within 72 hours, or obstetric brachial plexus injury.” The trial randomly assigned 1381 women to the induction group and 1379 women to the expectant management group. For the primary outcome measure, the trial found no effect: “The composite primary perinatal outcome did not differ between the groups: 2.4% (33/1381) in the induction group and 2.2% (31/1379) in the expectant management group.” However, the trial was stopped early, because six perinatal deaths occurred in the expectant management group, whereas none occurred in the induction group ( $P=0.03$ )¹. As the authors describe, “On 2 October 2018 the Data and Safety Monitoring Board strongly recommended the SWEPIS steering committee to stop the study owing to a statistically significant higher perinatal mortality in the expectant management group. Although perinatal mortality was a secondary outcome, it was not considered ethical to continue the study.” The authors conclude that “Although these results should be interpreted cautiously, induction of labour ought to be offered to women no later than at 41 weeks and could be one (of few) interventions that reduces the rate of stillbirths.”

The $p$ -value of Wennerholm and colleagues leaves unaddressed the extent to which the data undercut or support the hypothesis that induction at 41 weeks reduces the rate of stillbirths. This is important, because if the evidence turns out to be weak, then it may be argued that the SWEPIS trial was stopped prematurely, and the SWEPIS data offer limited grounds for changing medical practice.

Here we conduct a Bayesian test for two proportions (Kass & Vaidyanathan, 1992; Gronau et al., 2019; i.e., logistic regression with group membership as the predictor) to quantify the evidence from the SWEPIS trial that induction of labour at 41 weeks reduces the rate of stillbirths. Under the no-effect model $H_{0}$ , the log odds ratio equals $\psi = 0$ , whereas under the positive-effect model $H_{+}$ , $\psi$ is assigned a positive-only normal prior $N_{+}( \mu, \sigma^{2})$ . A default analysis (i.e., $\mu = 0, \sigma=1$ ) reveals moderate evidence for $H_{+}$ : the data are 3.32 times more likely under the hypothesis that induction at 41 weeks is beneficial than under the hypothesis that it is ineffective. When $H_{0}$ and $H_{+}$ are deemed equally likely a priori, this observed level of evidence increases the probability for $H_{+}$ from 0.50 to 0.77, leaving a sizable probability of 0.23 for $H_{0}$ .

A sensitivity analysis examines the strength of the evidence for all $N_{+}( \mu, \sigma^{2})$ prior combinations of $\mu$ in $[0, 2.5]$ and $\sigma$ in $[0.1, 1]$ ; as is apparent from the legend of Figure 1, the evidence never exceeds 5.4. In other words, with equal prior probability for $H_{0}$ and $H_{+}$ , the posterior probability for $H_{0}$ is never less than 0.16.

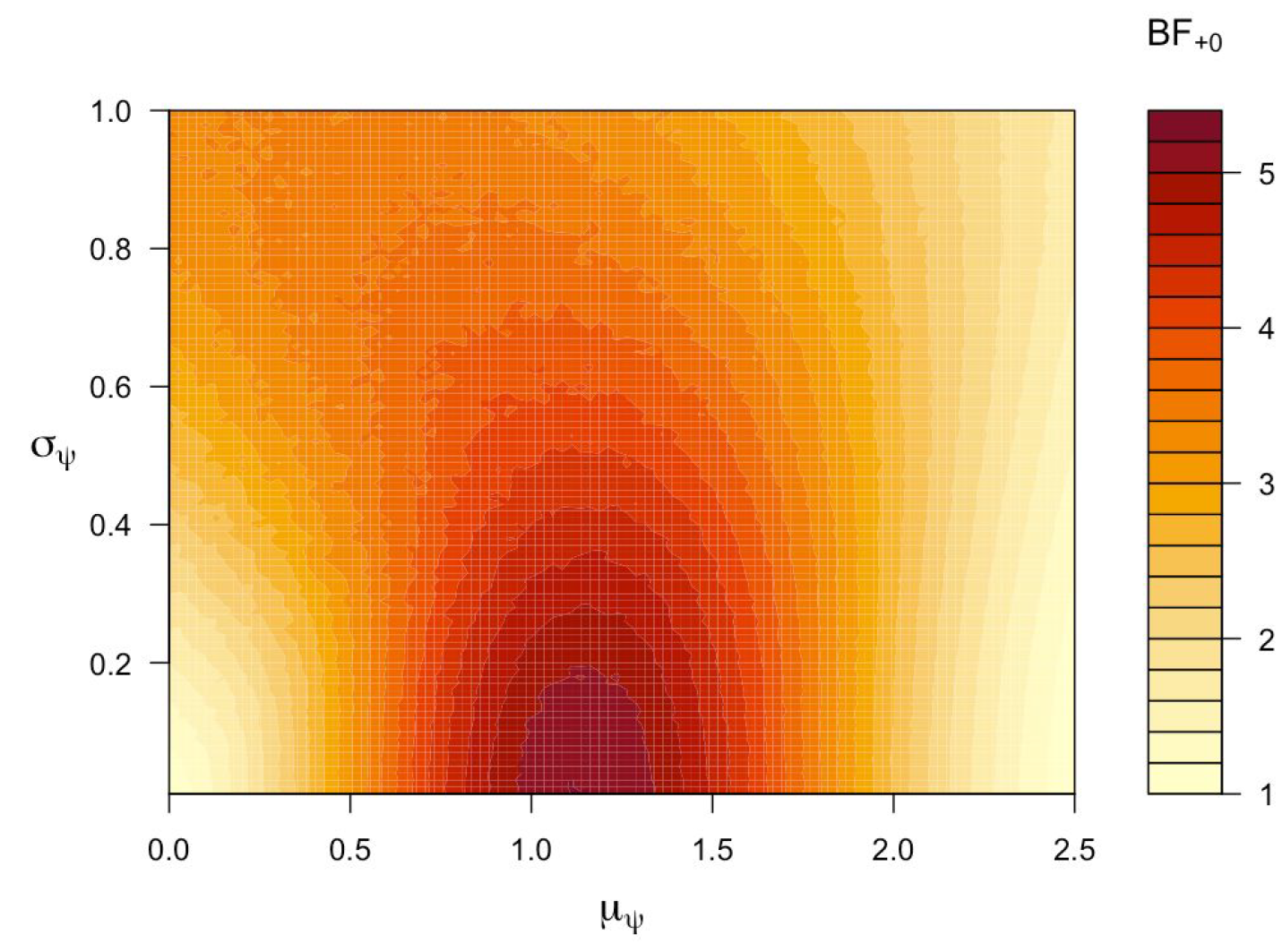
Figure 1. Across a range of different priors, the evidence for the positive-effect $H_{+}$ over the no-effect $H_{0}$ is relatively weak and does not exceed 5.4. Figure from JASP.

In addition to hypothesis testing one may also inspect the posterior distribution for $\psi$ under a two-sided model that assigns $\psi$ a standard normal distribution prior to data observation. As Figure 2 shows, the posterior distribution is relatively wide (note that this distribution ignores the possibility that $\psi=0$ exactly).

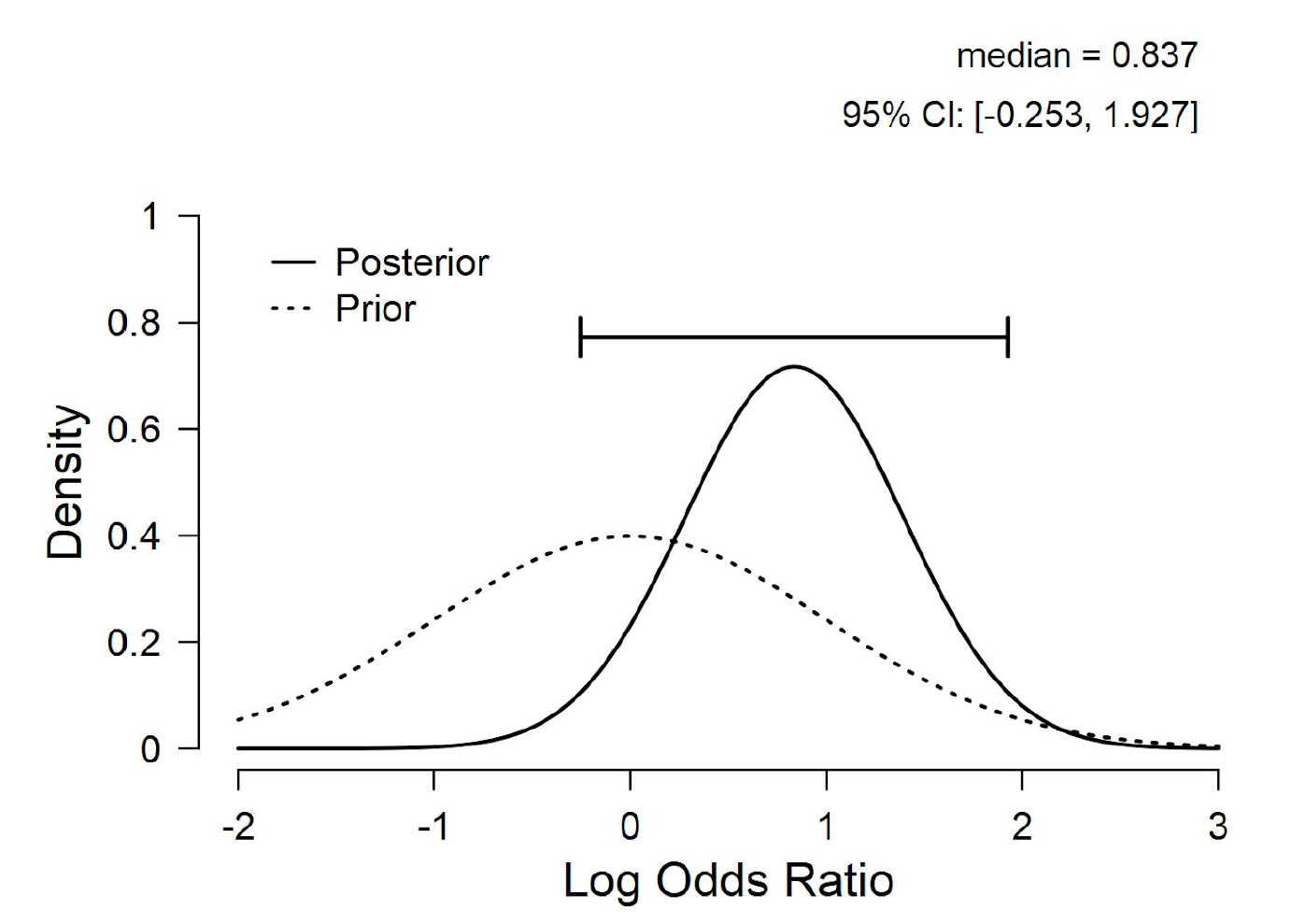
Figure 2. Prior and posterior distribution for the log odds ratio $\psi$ for an unconstrained model that assigns $\psi$ a standard normal distribution. Figure from JASP.

In sum, the SWEPIS data indeed support the hypothesis that induction of labour at 41 weeks of pregnancy is associated with a lower rate of stillbirths. However, the degree of this support is moderate at best, and arguably provides insufficient ground for terminating the study. Note that premature study termination comes at a cost — here, the cost is that the experiment ended up providing ambiguous results that yield a poor basis for changes in medical policy, leaving the field in epistemic limbo. In general, it seems hazardous to terminate clinical studies on the basis of a single $p<.05$ result, without converging support of a Bayesian analysis.

Notes

¹ Our analysis yields $P=.015$ . Because the induction group has zero perinatal deaths, the one-sided $P$ -value equals the two-sided $P$ -value.

References

Gronau, Q. F., Raj, K. N. A., & Wagenmakers, E.J. (2019). Informed Bayesian inference
for the A/B test. Manuscript submitted for publication and available on ArXiv: http://arxiv.org/abs/1905.02068.

Kass R. E., & Vaidyanathan, S. K. (1992). Approximate Bayes factors and orthogonal parameters, with application to testing equality of two binomial proportions. Journal of the Royal Statistical Society: Series B (Methodological). 54(1):129-144.

Wagenmakers, E.-J., & Ly, A. (2020). Bayesian scepsis about SWEPIS: Quantifying the evidence that early induction of labour prevents perinatal deaths.

Wennerholm, U. B., Saltvedt, S., Wessberg, A., et al. (2019). Induction of labour at 41 weeks versus expectant management and induction of labour at 42 weeks (SWEdish Post-term Induction Study, SWEPIS): Multicentre, open label, randomised, superiority trial. BMJ, 367:l6131.

About The Authors

Eric-Jan Wagenmakers

Eric-Jan (EJ) Wagenmakers is professor at the Psychological Methods Group at the University of Amsterdam.

Alexander Ly

Alexander Ly is a postdoc at the Psychological Methods Group at the University of Amsterdam.

Blog

Bayesian Scepsis About SWEPIS: Quantifying the Evidence That Early Induction of Labour Prevents Perinatal Deaths

Search

Categories

follow us