This post is an extended synopsis of van Doorn, J. B., Matzke D., & Wagenmakers, E.-J. (in press). An In-Class Demonstration of Bayesian Inference. Psychology Learning and Teaching (https://doi.org/10.1177/14757
25719848574). Preprint available on PsyArXiv:https://psyarxiv.com/d8bvn/

Abstract

Over 80 years ago, Sir Ronald Fisher conducted the famous experiment “The Lady Tasting Tea” in order to test whether his colleague, Dr. Muriel Bristol, could taste if the tea infusion or the milk had been added to the cup firs. Dr. Bristol was presented with eight cups of tea and the knowledge that four of these had the milk poured in first. Dr. Bristol was then asked to identify these four cups. We revisit Fisher’s experimental paradigm and demonstrate how a similar tasting experiment, conducted in a classroom setting, can familiarize students with several key concepts of Bayesian inference, such as the prior distribution, the posterior distribution, the Bayes factor, and sequential analysis.

The Experiment

On a Friday afternoon, May 12th 2017, an informal beer tasting experiment took place at the Psychology Department of the University of Amsterdam. The experimental team consisted of three members: one to introduce the participants to the experiment and administer the test, one to pour the drinks, and one to process the data. Participants tasted two small cups filled with Weihenstephaner Hefeweissbier, one with alcohol and one without, and indicated which one contained alcohol. We note that beer can be substituted with anything else suitable (e.g., red and green M&M’s, Coca Cola and Pepsi, decaf and regular coffee).

The experiment was double-blind, such that the person administering the test and interacting with the participants did not know which of the two cups contained alcohol. For ease of reference, each cup was labeled with a random integer between 1 and 500, and each integer corresponded either to the alcoholic or non-alcoholic beer. A coin was flipped to decide which beer was tasted first.

Analysis

Of the 57 participants, 42 (73.7%) correctly identified the beer that contained alcohol: in other words, there were successes and failures. In order to assess statistically whether and to what extent participants were able to discriminate between alcoholic and non-alcoholic beer we apply the binomial model, where the rate parameter governs the probability of a correct response for each of the participants.
Chance performance corresponds to . Above-chance performance corresponds to values of higher than , with indicating perfect performance.

In order to analyze the collected data, the Bayesian binomial test in JASP can be used, which can be found under the menu labeled “Frequencies”. Several settings are available for the binomial test, allowing students to explore different analysis choices.
Figure 1 presents a screenshot of the options panel in JASP. For this analysis, we specify a test value of (i.e., chance performance)and for the prior distribution of under the alternative hypothesis. Note that in a sensitivity or robustness analysis, other values for and may be explored to assess their impact on the posterior distribution. Since we wish to test whether or not participants’ discriminating ability exceeds chance, we can specify the alternative hypothesis to allow only values of greater than .

Figure 2 illustrates the results of the binomial test. Here we show the prior and the posterior distribution of for the one-sided alternative hypothesis, along with the median and credible interval of the posterior distribution. The posterior median equals and the credible interval ranges from to , indicating a substantial deviation of from . For each value of , the change from prior distribution to posterior distribution is quantified by predictive adequacy: for those values of that predict the data better than average, the posterior density exceeds the prior density.
The one-sided positive hypothesis (i.e., ) outperforms the null hypothesis: the resulting Bayes factor is in favor of the alternative hypothesis, that is, the observed data are about times more likely to occur under than under . We can therefore conclude that psychologists are able to distinguish alcoholic beer from non-alcoholic beer.

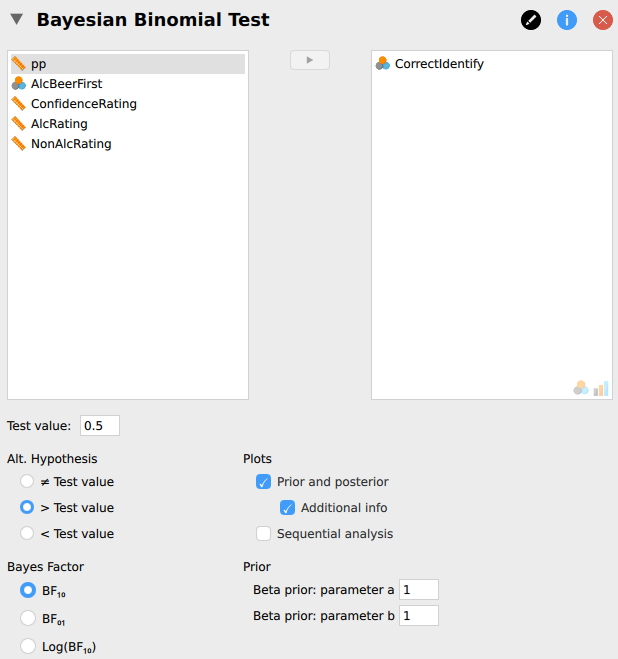
Figure 1. The input panel for the Bayesian binomial test in JASP. The upper left box displays all available variables. The upper right box displays the tested variables. Below are other options, such as setting the test value, the alternative hypothesis, and the shape parameters of the beta prior.

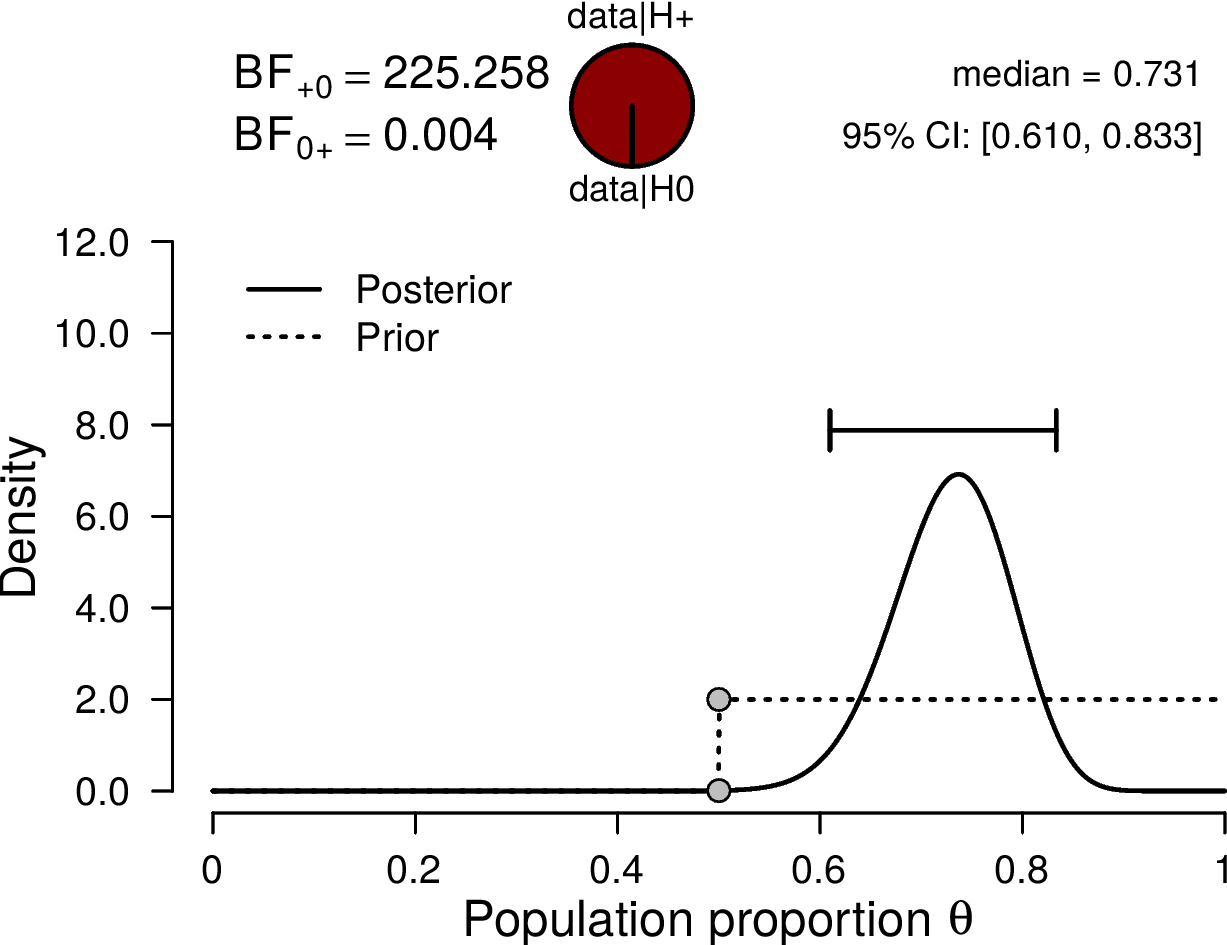
Figure 2. Bayesian binomial test for the rate parameter . The probability wheel at the top illustrates the ratio of the evidence in favor of the two hypotheses. The two gray dots indicate the prior and posterior density at the test value – the ratio of these is the Savage-Dickey density ratio. The median and the credible interval of the posterior distribution are shown in the top right corner.

Concluding Comments

This article has outlined a teaching tool for familiarizing students with the basics of Bayesian inference. The educational advantage of the Bayesian binomial test is that both the likelihood function and the parameterization of the prior and posterior distributions are intuitive and straightforward. The tasting experiment allows students to analyze their own data, collected on the fly, making the inferential process more concrete and relevant.

Table 1 summarizes the concepts that are introduced during the tasting experiment, as well as how these concepts can be practically demonstrated. The experiment is aimed at introducing college level students to these concepts. We have positive experiences using it as a teaching tool in both introductory workshops and undergraduate courses in Bayesian inference. We have created an Open Science Framework repository that contains the original data set, as well as a fully annotated JASP-file. The repository can be found at https://osf.io/428pb/. Finally, we would like to thank Ronald Fisher for proposing the experimental procedure, and Dennis Lindley for shedding a Bayesian light on it. Without their seminal works we would not have been able to conclude that most psychologists are able to taste the difference between alcoholic and non-alcoholic beer.

Bayesian Concept	Demonstration
Irrelevance of sampling plan for Bayesian updating	Analyzing the data as they come in
Evidence for is possible, as it is for	Computing the Bayes factor
Conjugate prior distribution	Using the binomial likelihood to update a beta prior distribution
Savage-Dickey density ratio for computation of Bayes factors	Interpreting posterior plots (e.g., Figure 2)
Analysis of sensitivity of results to choice of prior distribution	Changing the parameters of the beta prior distribution and observing the corresponding changes in the posterior distribution and the Bayes factor
Bayesian one-sided testing	Specifying different alternative hypotheses
Principle of parsimony in Bayesian inference	Comparing two-sided results with one-sided results

Table 1. Bayesian concepts that students will learn during the tasting experiment and how these concepts can be demonstrated.

References

van Doorn, J.B., Matzke D., & Wagenmakers, E.-J. (in press). An In-Class Demonstration of Bayesian Inference. Psychology Learning and Teaching. Preprint available on PsyArXiv: https://psyarxiv.com/d8bvn/

Fisher, R. A. (1937). The design of experiments. Oliver And Boyd; Edinburgh;
London.

Lindley, D. V. (1993). The analysis of experimental data: The appreciation of
tea and wine. Teaching Statistics, 15 , 22–25.

About The Author

Johnny van Doorn

Johnny van Doorn is a PhD candidate at the Psychological Methods department of the University of Amsterdam.

Dora Matzke

Dora Matzke is an assistant professor at the Psychological Methods department of the University of Amsterdam.

Eric-Jan Wagenmakers

Eric-Jan (EJ) Wagenmakers is professor at the Psychological Methods Group at the University of Amsterdam.