Preprint: Evaluating Multinomial Order Restrictions with Bridge Sampling
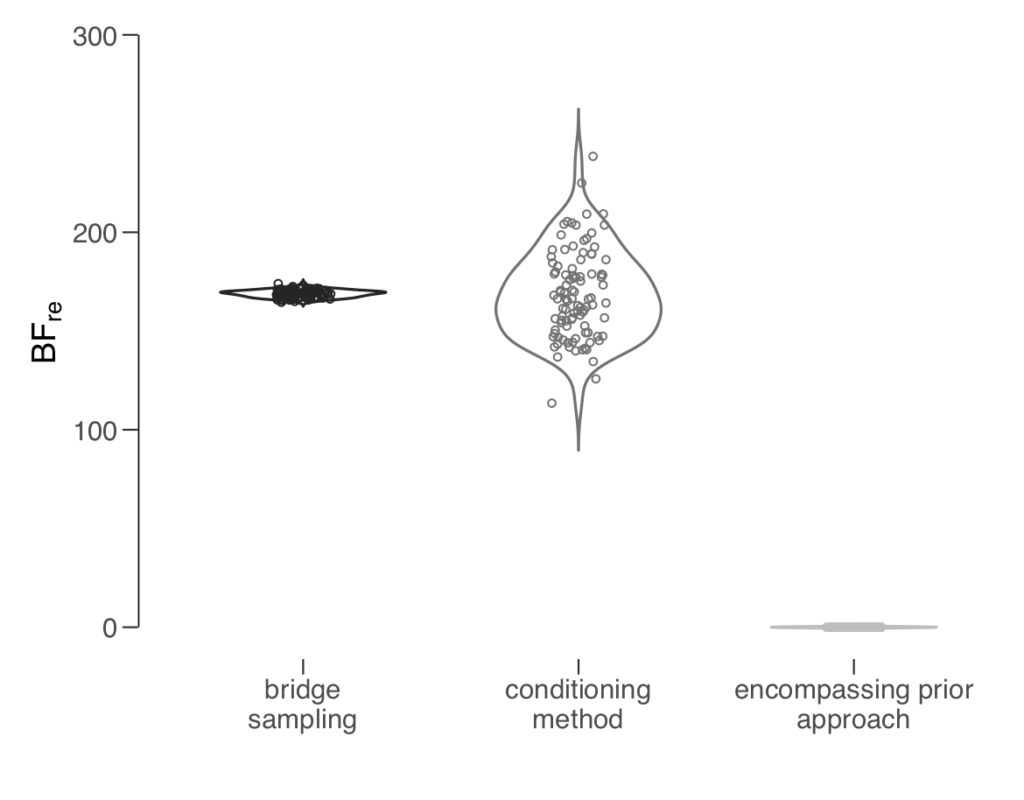
This post is a teaser for Sarafoglou, A., Haaf, J. M., Ly, A., Gronau, Q. F., Wagenmakers, E.-J., & Marsman, M. (2020). Evaluating multinomial order restrictions with bridge sampling. Preprint available on PsyArXiv: https://psyarxiv./bux7p/ Summary Hypotheses concerning the distribution of multinomial proportions typically entail exact equality constraints that can be evaluated using standard tests. Whenever researchers formulate inequality constrained hypotheses,…
read more