In the past months, SpaceX was quickly moving forward with development of their interplanetary rocket – Starship. The last two prototypes even went ahead with a test flight to ~10 km. The test flight was, in both cases, highly successful, apart from ending in an RUD (rapid unscheduled disassembly) during the landing. That was not unexpected since the previous prototypes had a low chance for successful landing, according to Elon Musk. Nevertheless, many people (and we) are wondering whether the next prototype (SN10), scheduled to attempt the test flight and landing procedure in the upcoming weeks, will finally stick the landing.

A recent twitter poll of almost 40,000 people estimated the probability of SN10 successfully landing at 77.5% (after removing people who abstained from voting).

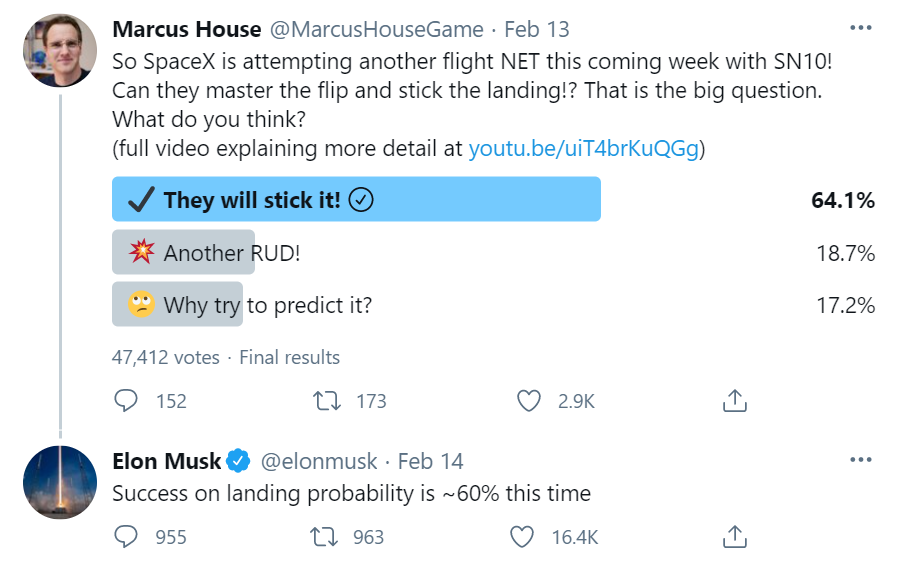
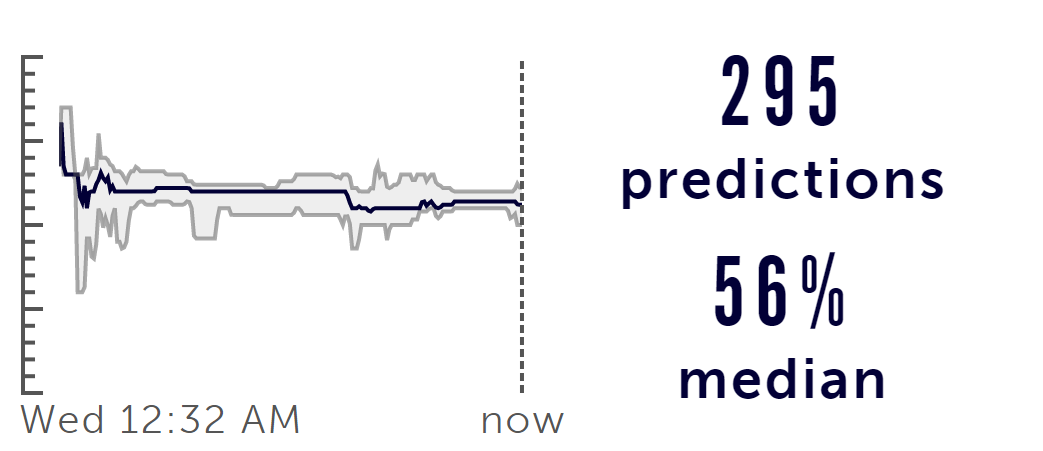
A much higher chance that Elon’s own estimate of ~60% which is comparable to the Metaculus prediction market based on 295 predictions that converged to 56% median probability of successful landing.

Here, we also try to predict whether the next Starship, SN10, will successfully land. As all statisticians, we start by replacing a difficult problem with a simpler one — instead of landing, we will predict whether the SN10 will successfully fire at least two of its engines as it approaches landing. Since the rocket engine can either fire up or malfunction, we approximate the engine firing up as a binomial event with probability θ. Starship prototypes have 3 rocket engines, out of which 2 are needed for successful landing. However, in previous landing attempts, SpaceX tried lighting up only 2 engines — both of which are required to fire up successfully. Now, in order to improve their landing chances, SpaceX decided to try lighting up all 3 engines and shutting down 1 of them if all fire successfully¹. We will therefore approximate the successful landing as observing 2 successful binomial events out of 3 trials. 

To obtain the predictions, we will use Bayesian statistics and specify a prior distribution for the binomial probability parameter θ, an engine successfully firing up. Luckily, we can easily obtain the prior distribution from the two previous landing attempts:

• The first Starship prototype attempting landing, SN8, managed to fire both engines, however, crashed due to low oxygen pressure resulting. That resulted in insufficient trust and way too fast approach to the landing site. Video [here].
• The second Starship prototype attempting landing, SN9, did not manage to fire the second engine which, again, resulted in an RUD on approach. Video [here].

Adding an additional assumption of the events being independent, we can summarize the previous firing up attempts with beta(4, 2) distribution — corresponding to observing 3 successful and 1 unsuccessful event. In JASP, we can use the Learn Bayes module to plot our prior distribution for θ

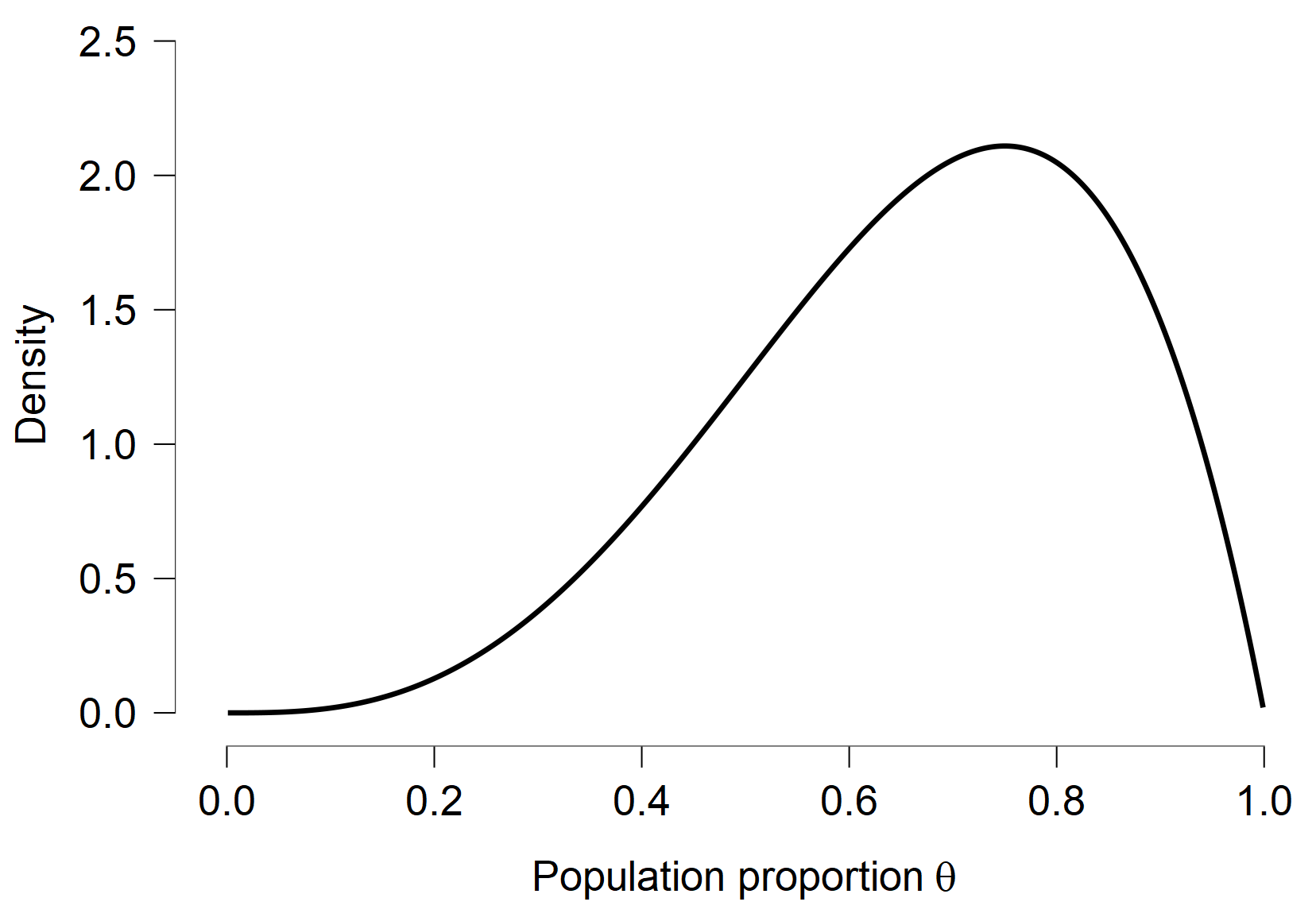
and generate predictions for 3 future events. Since the prior distribution for θ is beta and we observe binomial events, the distribution of number of future successes based on 3 observations follows a beta-binomial(3, 4, 2) distribution. We obtain a figure depicting the predicted number of successes from JASP and we further request the probability of observing at least two of them. Finally, we arrive at an optimistic prediction of 71% chance of observing at least 2 of the engines fire up on the landing approach. Of course, we should treat our estimate as a higher bound on the actual probability of successful landing. There are many other things that can go wrong (see SpaceX’s demonstration [here]) that we did not account for (in contrast to SpaceX, we are not trying to do a rocket science here). 

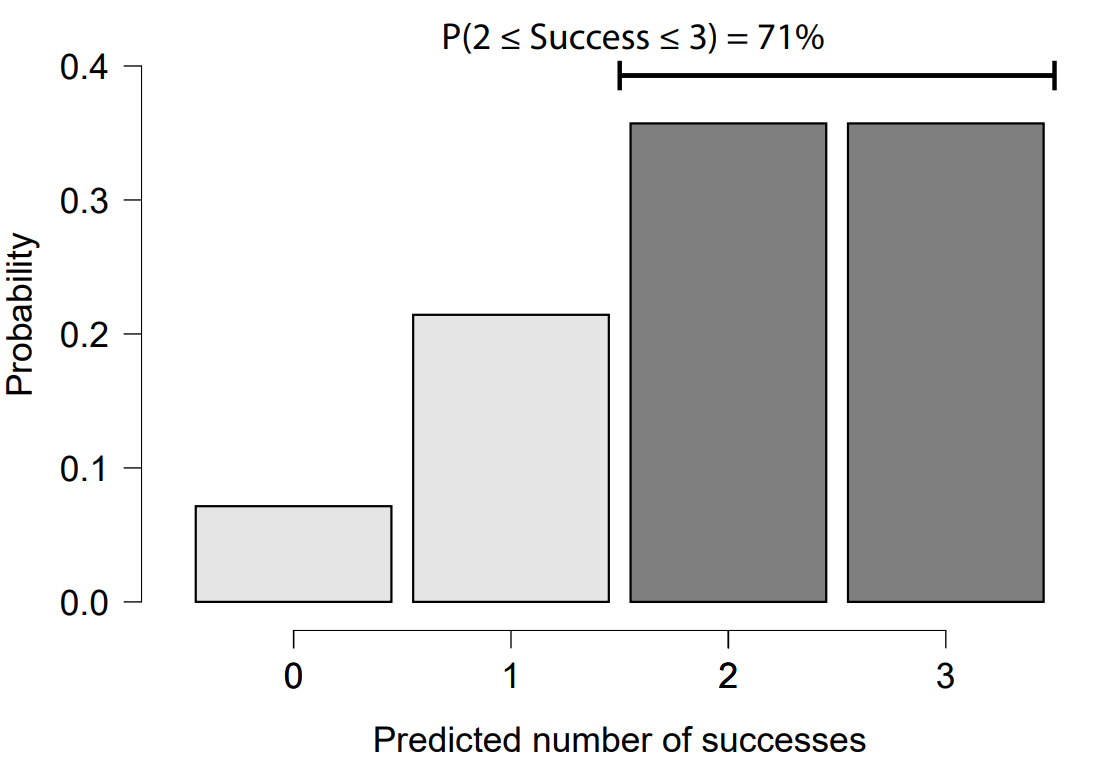
We can also ask how much does trying to fire up all 3 engines instead of 2 (as in previous attempts) increase the chance of successful landing. For that, we just need to obtain the probability of observing at 2 successful events based on 2 observations = 48% (analogously from beta-binomial(2, 4, 2) distribution), and subtract it from the previous estimate of 71%. That is a 23% higher chance of landing when trying to use all 3 instead of only 2 engines.

About The Authors

František Bartoš

František Bartoš is a Research Master student in psychology at the University of Amsterdam.

 

1. Spaceship prototypes cannot land with all three engines — the engines have too much trust and decreasing the trust below a certain threshold would result in an automatic engine shutdown.