A Geometric Intuition for the Logarithm

The logarithm is a key concept in mathematics and statistics. Most students will be introduced to the logarithm as the function that is the inverse of exponentiation, or the function that turns multiplication into addition. But without a good intuition of what the logarithm actually is, students can struggle to remember how to compute the logarithm of base r for a number v. Speaking for myself, I generally had to look up the definition every time — which is a sure sign that you don’t properly understand the concept. The definition is as follows:

v = r^d \Rightarrow d = \log_r(v).

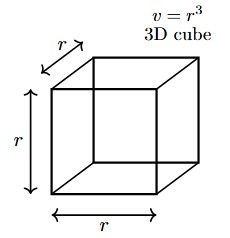
Luckily there exists a simple geometric intuition for the logarithm. The only object we need is a “hypercube“, an d-dimensional object with equal sides. As shown in the figure below, a hypercube of dimension d=1 is a line; a hypercube of dimension d=2 is a square, and a hypercube of dimension d=3 is a cube (etc.). Let’s call the length of the constituent line segments ‘r’ for root, the basic component from which the hypercube grows. The volume of a hypercube is computed by multiplying the line segment r a total of d times, such that v = r^d. For instance, when r=10 and d=3, we have a cube of volume v = 10^3 = 1000.

Most people will be familiar with the “volume rule”. However, this common rule specifies a relation between three quantities: volume v, root line length r, and dimension d. When two quantities are known, the third is given. This means we may also ask “given a volume v and a dimension d, what is the length of the line segment r?” For instance, if v=1000 and d=3, we may compute that r=10. Mathematically, we have that

v = r^d \Rightarrow r = \sqrt[d]v = v^{1/d};

in words, r is the dth root of v. One question remains: given a volume v and a line segment of length r, what is the dimension d of the hypercube? For instance, if v=1000 and r=10, we may compute that d=3. This answer is in fact the logarithm of v with base r, that is:

v = r^d \Rightarrow d = \log_r(v).

This geometric intuition also makes it easy to see how the logarithm turns multiplication into addition. Consider how a hypercube unfolds as the dimensionality d increases. Every time a new dimension is added, the volume multiplies. With a root length r, the unfolding multiplicative sequence v = r \times r \times r \times r \dots maps onto a simple additive sequence d = 1 + 1 + 1 +1 \dots .

Strangely I have not come across this simple geometric idea before. Mathematicians will no doubt find it too obvious to state. Nevertheless, I think it may benefit the student (as it benefitted me). Of course the geometry is less intuitive for fractional dimensions, but the purpose of the example is to be helpful rather than comprehensive.

Eric-Jan Wagenmakers

Eric-Jan (EJ) Wagenmakers is professor at the Psychological Methods Group at the University of Amsterdam.