Preprint: Computing and Using Inclusion Bayes Factors for Mixed Fixed and Random Effect Diffusion Decision Models
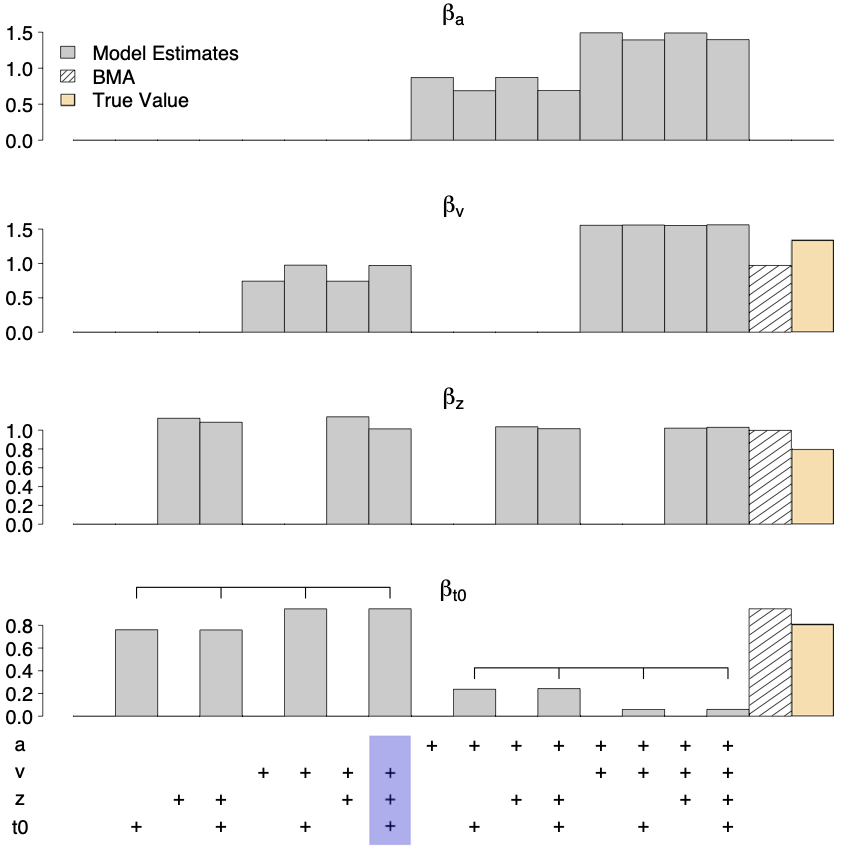
This post is a synopsis of Boehm U, Evans N J, Gronau D., Matzke D, Wagenmakers E.-J., & Heathcote A J. (2021). Computing and using inclusion Bayes factors for mixed fixed and random effect diffusion decision models. Preprint available at https://psyarxiv.com/45t2w Abstract Cognitive models provide a substantively meaningful quantitative description of latent cognitive processes. The quantitative formulation of these models…
read more