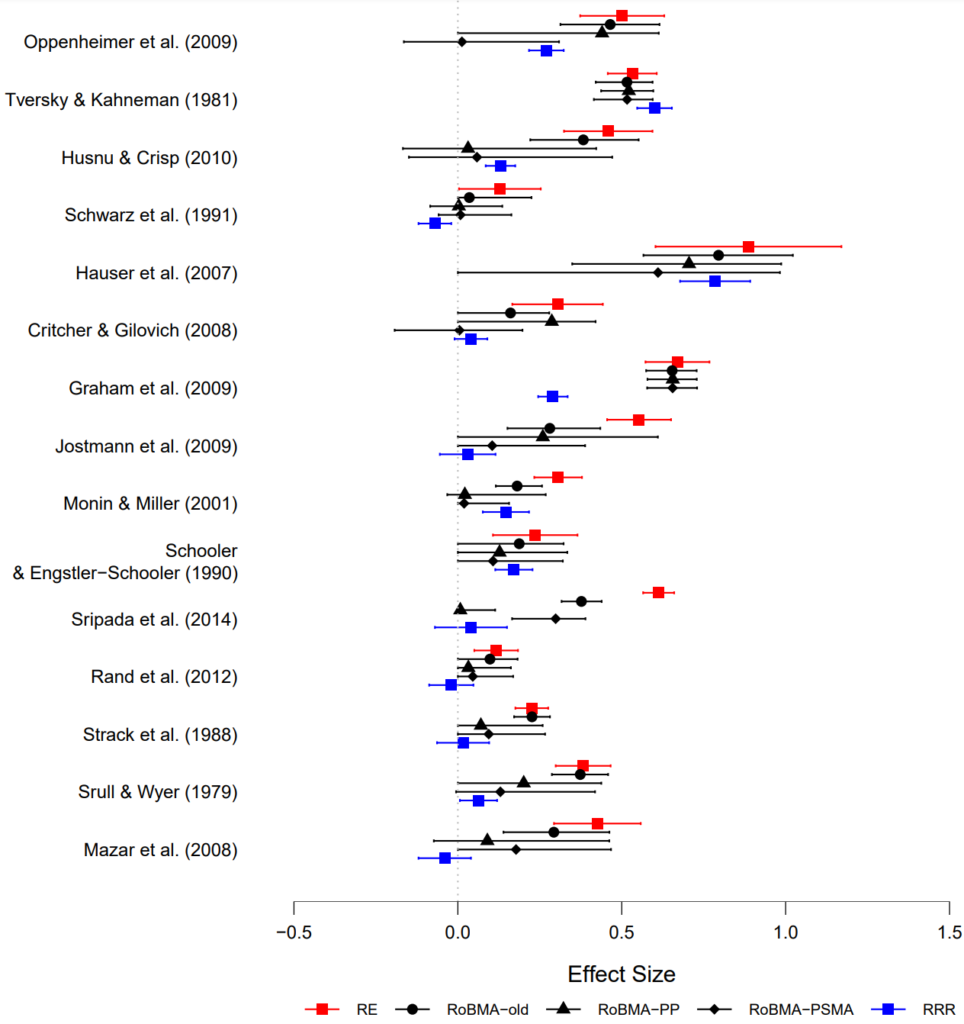
This post is a synopsis of Bartoš, F, Maximilian M, Wagenmakers E.-J., Doucouliagos H., & Stanley, T D. (2021). No need to choose: Robust Bayesian meta-analysis with competing publication bias adjustment methods. Preprint available at https://doi.org/10.31234/osf.io/kvsp7 Abstract “Publication bias is a ubiquitous threat to the validity of meta-analysis and the accumulation of scientific evidence. In order to estimate and counteract…